Tamanho da Amostra, Variância e Viés¶
Uma vez que as observações são independentes (independents) e a distribuição da população (population) destas observações não é muito enviesada (skewed), então, o fato de termos amostras aleatórias (random samples) grandes garante que:
- Teremos uma distribuição amostral (sampling distribution) de médias $\bar{X}$ que é aproximadamente Normal (como já foi visto aqui);
- A estimativa para o erro padrão (standard error) $SE$ desta distribuição amostral (sampling distribution) será confiável (como já foi visto aqui).
Em outras palavras, pelo Teorema Central do Limite (Central Limit Theorem - CLT) teremos que esta distribuição amostral (sampling distribution) das médias $\bar{X}$ que é aproximadamente normal (nearly normal) será também, centrada na média $\mu$ da população (population), e com um desvio padrão (standard deviation) igual ao desvio padrão (standard deviation) $\sigma$ da população (population) dividido pela raiz quadrada do tamanho $n$ da amostra.
$$ \bar{X} \sim N\left(mean=\mu, SE=\frac{\sigma}{\sqrt{n}}\right) $$Porém, como dificilmente tem-se acesso à população (population), então, tipicamente o desvio padrão (standard deviation) $\sigma$ da população (population) é desconhecido. Geralmente, tem-se acesso a uma amostra aleatória (random sample) de tamanho $n$ ($x = \{ x_1, x_2, \ldots, x_n \}$) e, por isto, costuma-se realizar as seguintes aproximações:
$$ \mu \approx \bar{x} $$$$ SE \approx \hat{se} = \frac{s}{\sqrt{n}} $$onde $\bar{x}$ representa a média da amostra aleatória (random sample) $x = \{ x_1, x_2, \ldots, x_n \}$ de tamanho $n$; e $s$ representa o desvio padrão (standard deviation) desta amostra aleatória (random sample).
No entanto, há dois pontos relacionados com o descrito anteriormente cuja falta de entendimento dos mesmos pode levar a erros de análise e tomada de decisão. Os dois pontos são:
- O desconhecimento da relação existente entre o tamanho da amostra $n$ e a variação $s$ presente dentro desta amostra dada pela fórmula $\hat{se} = \frac{s}{\sqrt{n}}$.
- Amostras ao mesmo tempo muito grandes e enviesadas.
A relação entre o tamanho da amostra e a variação da mesma¶
Em 2007 foi publicado na Sigma Xi, The Sientific Research Socienty o artigo entitulado The Most Dangerous Equation - Ignorance of how sample size affects statistical variation has created havoc for nearly a millennium (link). Neste artigo, a equação que é considerada a mais perigosa para o autor é a
$$ \sigma_\bar{x} = \frac{s}{\sqrt{n}} $$onde $\sigma_\bar{x}$ é o erro padrão (standard error) da média, $s$ é o desvio padrão (standard deviation) da amostra aleatória (random sample) e $n$ é o tamanho da amostra aleatória (random sample). Isto é, exatamente a equação que vimos anteriormente para a aproximação $\hat{se}$ do erro padrão (standard error) da média.
Esta equação releva que:
- A variabilidade ($s$) nos dados aumenta proporcionalmente à raíz quadrada do tamanho da amostra ($\sqrt{n}$), ao invés de proporcionalmente ao tamanho $n$ da amostra (como muitos acreditam que seja o caso).
- A variação ($SE = \sigma_\bar{x}$) da média é inversamente proporcional à raíz quadrada do tamanho da amostra ($\sqrt{n}$), ou seja, amostras pequenas apresentam uma variação muito maior do que amostras muito grandes.
O artigo The Most Dangerous Equation apresenta 5 exemplos onde estas duas interpretações acima são ignoradas e, em virtude disto, consequências sérias ou até mesmo desastrosas ocorreram. Aqui, vamos verificar 2 destes 5 exemplos.
Exemplo 1: The Trial of the Pyx¶
Em 1150, foi reconhecido que o rei da Inglaterra não poderia simplesmente cunhar moedas e designá-las para ter qualquer valor que escolhesse. Em vez disso, o valor da cunhagem precisava ter relação com a quantidade de materiais preciosos em sua composição. Então, foram estabelecidos padrões para o peso do ouro em moedas - 1 guinéu (guinea), por exemplo, deveria pesar $128$ gramas. No teste do pyx -- o pyx é na verdade a caixa de madeira que contém as moedas padrão - as amostras são medidas e comparadas com o padrão.
Reconheceu-se, mesmo assim, que os métodos de cunhagem eram muito imprecisos para insistir que todas as moedas fossem exatamente iguais em peso, então o rei e os barões que abasteciam a Casa da Moeda de Londres com ouro insistiam que as moedas fossem testadas de modo agregado (digamos $100$ de cada vez) em conformidade com o tamanho regulado mais ou menos alguma margem de variação. Eles escolheram $\frac{1}{400}$ do peso, o que para 1 guinéu (guinea) seria $0,32$ gramas e, portanto, para o agregado de $100$ moedas, $320$ gramas. Obviamente, eles assumiram, de modo errado, que a variabilidade aumentava proporcionalmente à quantidade de moedas e não à sua raiz quadrada, como a equação $\sigma_\bar{x} = \frac{s}{\sqrt{n}}$ mais tarde indicaria. Esse entendimento equivocado durou quase 600 anos no futuro.
guinea_standard_weight_coin = 128
allowance_threshold_for_weight_variability = 1/400.0
allowance_threshold_for_1_guinea = guinea_standard_weight_coin * allowance_threshold_for_weight_variability
print("Weight of 1 guinea = {0}".format(guinea_standard_weight_coin))
print("Allowance threshold for 1 guinea = {0}".format(allowance_threshold_for_1_guinea))
print("Inferior threshold = {0}".format(guinea_standard_weight_coin - allowance_threshold_for_1_guinea))
print("Superior threshold = {0}".format(guinea_standard_weight_coin + allowance_threshold_for_1_guinea))
Os custos de cometer erros são de dois tipos. Se a média de todas as moedas fosse muito leve, os barões estavam sendo enganados, pois sobraria ouro extra depois de cunhar o número acordado de moedas. Esse tipo de erro é facilmente detectado e, se encontrado, o diretor da Casa da Moeda sofreria severos castigos. Mas se a variabilidade permitida fosse maior do que o necessário, haveria um número excessivo de moedas muito pesadas, neste caso, a Casa da Moeda poderia, portanto, ficar dentro dos limites especificados e ainda fornecer a oportunidade para alguém de lá recolher essas moedas com excesso de peso, derretê-las e reformulá-las com o menor peso padrão. Isso deixaria o saldo de ouro como um pagamento em excesso para a casa da moeda.
Para verificarmos isto, suponha um conjunto de $1.000$ moedas cujos pesos variam ao redor (noise) de $128$ (guinea_standard_weight_coin) gramas de forma que esta variação possa ser composta por moedas até $3,16$ vezes mais ou menos pesadas do que o peso padrão de $128$ gramas.
from scipy import stats as st
quantity_of_coins = 1000
# noise varying randomly between -1 to 1 to simulate variation around the 128 grammas
noise = st.uniform(loc=-1, scale=2).rvs(quantity_of_coins, random_state=1234)
# simulated set of 1000 coins varying around the standard weight (128 grammas) of 1 guinea
coins_before_coinage = guinea_standard_weight_coin + (noise * 3.16 * allowance_threshold_for_1_guinea)
import numpy as np
import pandas as pd
import altair as alt
alt.renderers.enable('notebook') # for the notebook only (not for JupyterLab) run this command once per session
def plot_coins(coins, guinea_standard_weight_coin, allowance_threshold_for_1_guinea):
# random noise in y to facilitates visualization
rand = np.random.RandomState(4321)
y = rand.rand(len(coins))
data = pd.DataFrame({
'coin_weight': coins,
'standard_weight': guinea_standard_weight_coin,
'variability_threshold': allowance_threshold_for_1_guinea,
'y': y
})
coins_plot = alt.Chart(data).mark_circle().encode(
alt.X('coin_weight:Q', scale=alt.Scale(zero=False)),
y='y'
)
standard_weight_mark = alt.Chart(data).mark_rule(color='red').encode(
x='standard_weight',
size=alt.value(1)
)
threshold_inf_mark = alt.Chart(data).mark_rule(color='orange').encode(
x='thresh_inf:Q',
size=alt.value(1)
).transform_calculate(
thresh_inf='datum.standard_weight - datum.variability_threshold'
)
threshold_sup_mark = alt.Chart(data).mark_rule(color='orange').encode(
x='thresh_sup:Q',
size=alt.value(1)
).transform_calculate(
thresh_sup='datum.standard_weight + datum.variability_threshold'
)
return coins_plot + (standard_weight_mark + threshold_inf_mark + threshold_sup_mark)
plot_coins(coins_before_coinage, guinea_standard_weight_coin, allowance_threshold_for_1_guinea)
No gráfico acima o eixo $x$ representa o peso das moedas ao passo que o eixo $y$ representa apenas um número aleatório entre $0$ e $1$ para espalhar os $1.000$ pontos azuis (as moedas) e, assim, facilitar a visualização. A linha vermelha representa a marcação para o peso padrão de $1$ guinéu (guinea), ou seja, $128$ gramas. As linhas de cor laranja representam a margem de variação permitida para o peso de $1$ guinéu (guinea), ou seja, os limites inferior ($128 - 0,32$) e superior ($128 + 0,32$) desta margem de variação.
Visualmente, é possível perceber que há muitas moedas fora da margem de variação permitida. Para verificarmos quantas moedas obedecem a margem de variação permitida e quantas violam podemos utilizar a função test_coins_1_by_1 que irá testar $1$ moeda por vez.
def test_coins_1_by_1(coins, guinea_standard_weight_coin, allowance_threshold_for_1_guinea):
guinaes_ok = []
coins_inferior_weight = []
coins_superior_weight = []
for coin in coins:
diff = coin - guinea_standard_weight_coin
if (np.abs(diff) <= allowance_threshold_for_1_guinea) :
guinaes_ok.append(coin)
elif (diff > 0):
coins_superior_weight.append(coin)
else:
coins_inferior_weight.append(coin)
return coins_inferior_weight, guinaes_ok, coins_superior_weight
coins_inf_weight, guineas_ok, coins_sup_weight = test_coins_1_by_1(
coins_before_coinage, guinea_standard_weight_coin, allowance_threshold_for_1_guinea
)
count_inf = len(coins_inf_weight)
count_ok = len(guineas_ok)
count_sup = len(coins_sup_weight)
print("Number of true guinaes = {0} ({1:.2f}%)".format(count_ok, (count_ok/quantity_of_coins)*100.0))
print("Number of coins w/ less weight = {0} ({1:.2f}%)".format(count_inf, (count_inf/quantity_of_coins)*100.0))
print("Number of coins w/ more weight = {0} ({1:.2f}%)".format(count_sup, (count_sup/quantity_of_coins)*100.0))
Ou seja, se cada uma das $1.000$ moedas dos barões que foram entregues à Casa da Moeda para serem cunhadas fosse testada separadamente contra $1$ moeda padrão de $1$ guinéu (guinea), então, teríamos como resultado:
- $314$ moedas passariam no teste e seriam consideradas $1$ guinéu (guinea);
- $332$ moedas não passariam no teste pois estariam abaixo do peso padrão e fora da margem de variação permitida;
- $354$ moedas não passariam no teste pois estariam acima do peso padrão e fora da margem de variação permitida;
No entanto, testar $1$ moeda por vez seria um processo muito lento e, como já sabemos, o rei e os barões que abasteciam a Casa da Moeda insistiam que as moedas fossem testadas de modo agregado ($100$ de cada vez). Além disto, eles determinaram, erroneamente, que o limiar de variação para o agregado de $100$ moedas deveria ser $100$ vezes o valor do limiar para $1$ guinéu (guinea), ou seja, $32$ gramas ($0,32 \times 100$).
Como já observado também, este erro foi cometido em virtude da falta de conhecimento na época de que a variabilidade aumentava proporcionalmente à raiz quadrada da quantidade de moedas, como mostra a equação $\sigma_\bar{x} = \frac{s}{\sqrt{n}}$ (ou seja, $s = \sigma_\bar{x} \times \sqrt{n}$).
Então, a função test_coins_per_group foi implementada para verificarmos quantas moedas passariam no teste caso as mesmas fossem testadas de modo agregado, por exemplo, de $100$ em $100$.
def test_coins_per_group(group_size, coins, guinea_standard_weight_coin, allowance_threshold_for_n_guineas):
quantity_of_coins = len(coins)
standard_weight_group = group_size*guinea_standard_weight_coin
guineas_ok = []
for i in range(0, quantity_of_coins, group_size):
group_of_coins = coins[i:(i+group_size)]
absolute_diff = np.abs(np.sum(group_of_coins) - standard_weight_group)
if (absolute_diff <= allowance_threshold_for_n_guineas) :
guineas_ok.extend(group_of_coins)
return guineas_ok
coins_group_size = 100
wrong_allowance_threshold = coins_group_size * allowance_threshold_for_1_guinea
guineas_ok = test_coins_per_group(
coins_group_size, coins_before_coinage, guinea_standard_weight_coin, wrong_allowance_threshold
)
count_ok = len(guineas_ok)
print("Wrong allowance threshold for 100 guineas = {0}".format(wrong_allowance_threshold))
print("Number of true guineas = {0} ({1:.2f}%)".format(count_ok, (count_ok/quantity_of_coins)*100.0))
Ou seja, se as mesmas $1.000$ moedas dos barões que foram entregues à Casa da Moeda para serem cunhadas fossem testadas em grupos de $100$ moedas contra $100$ vezes o peso padrão de $1$ guinéu (guinea) considerando o limiar, equivocado, de variação de $32$ gramas ($0,32 \times 100$), então, teríamos como resultado:
- As $1.000$ moedas passariam no teste e seriam consideradas $1$ guinéu (guinea) cada;
O que já vimos que é errado, uma vez que no conjunto das $1.000$ moedas há apenas $314$ ($31,4\%$) moedas que passariam no teste individual.
Se naquela época existisse o conhecimento da relação dada pela equação $\sigma_\bar{x} = \frac{s}{\sqrt{n}}$, então, os grupos de $100$ moedas teriam como limiar de variação permitido o valor de $3,2$ gramas ($0,32 \times \sqrt{100}$) ao invés dos $32$ gramas ($0,32 \times 100$).
correct_allowance_threshold = np.sqrt(coins_group_size) * allowance_threshold_for_1_guinea
guineas_ok = test_coins_per_group(
coins_group_size, coins_before_coinage, guinea_standard_weight_coin, correct_allowance_threshold
)
count_ok = len(guineas_ok)
print("Correct allowance threshold for 100 guineas = {0}".format(correct_allowance_threshold))
print("Number of true guineas = {0} ({1:.2f}%)".format(count_ok, (count_ok/quantity_of_coins)*100.0))
Ou seja, se as mesmas $1.000$ moedas dos barões que foram entregues à Casa da Moeda para serem cunhadas fossem testadas em grupos de $100$ moedas contra $100$ vezes o peso padrão de $1$ guinéu (guinea) considerando o limiar, correto, de variação de $3,2$ gramas ($0,32 \times \sqrt{100}$), então, teríamos como resultado:
- Somente $300$ moedas passariam no teste e seriam consideradas $1$ guinéu (guinea) cada;
Ou seja, uma quantidade muito mais próxima das $314$ moedas que passariam no teste individual.
Exemplo 2: Life in the Country: Haven or Threat?¶
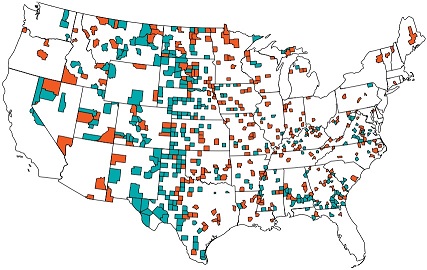(Fonte: The Most Dangerous Equation - Ignorance of how sample size affects statistical variation has created havoc for nearly a millennium, Howard Wainer, 2007.)
A figura acima é um mapa das localizações de municípios com taxas incomuns de câncer de rim (kidney-cancer). Os municípios verdes são aqueles que estão no decil mais baixo da distribuição do câncer, pode-se notar que esses municípios saudáveis tendem a ser muito rurais, do meio-oeste, sul ou oeste. É fácil e tentador inferir que esse resultado é diretamente devido à vida limpa do estilo de vida rural - sem poluição do ar, sem poluição da água, acesso a alimentos frescos sem aditivos e assim por diante.
Os municípios de cor vermelha, no entanto, desmentem essa inferência. Embora eles tenham a mesma distribuição que os municípios verdes - na verdade, eles são muitas vezes adjacentes - são aqueles que estão no mais alto decil da distribuição do câncer. Notamos que esses municípios insalubres tendem a ser muito rurais, do meio-oeste, sul ou oeste. Seria fácil inferir que esse resultado pode ser diretamente devido à pobreza do estilo de vida rural - nenhum acesso a bons cuidados médicos, uma dieta rica em gordura e muito álcool e tabaco.
Mas o que está acontecendo? Na prática, estamos vendo a equação $\sigma_\bar{x} = \frac{s}{\sqrt{n}}$ em ação. A variação da média é inversamente proporcional ao tamanho da amostra, de modo que os municípios pequenos exibem uma variação muito maior do que os grandes municípios. Um município com, digamos, 100 habitantes e sem mortes por câncer estaria no menor decil da distribuição da taxa de cancer, mas, se este mesmo município tiver 1 morte por câncer, então, ele estará entre os municípios com as mais altas taxas de cancer. Já, municípios com milhões de habitantes não apresentam este comportamento.
Para verificarmos isto, suponha um exemplo fictício em que a população de um dado país seja composta por $15.501.000$ habitantes e que neste país a probabilidade de alguém contrair cancer de rim seja de $0,5\%$, ou seja, $\Pr\left( \textrm{kidney-cancer} \right) = 0,005$.
random_seed = 1268
population_size = 15501000
# Use of the bernoulli distribution to generate a population of 15501000 inhabitants
# with probability 0.005 of contracting kidney-cancer.
prob_kidney_cancer = 0.005
bernoulli_dist = st.bernoulli(prob_kidney_cancer)
population = bernoulli_dist.rvs(size=population_size, random_state=random_seed)
total_cases_kidney_cancer = np.sum(population)
proportion_kidney_cancer = total_cases_kidney_cancer/float(population_size)
print("Total population of the fictitious country = {0}".format(population_size))
print("Total cases of kidney cancer = {0}".format(total_cases_kidney_cancer))
print("Proportion of kidney cancer = {0:.3f} ({1:.1f}%)".format(proportion_kidney_cancer, proportion_kidney_cancer*100))
Suponha também que neste país há $91$ municípios sendo que:
- $30$ deles possuem cerca de $5.000$ habitantes;
- $13$ deles possuem cerca de $27.000$ habitantes;
- $12$ deles possuem cerca de $50.000$ habitantes;
- $12$ deles possuem cerca de $150.000$ habitantes;
- $12$ deles possuem cerca de $300.000$ habitantes;
- $10$ deles possuem cerca de $500.000$ habitantes;
- $2$ deles possuem cerca de $2.000.000$ habitantes;
base_city_sizes = [5000, 27000, 50000, 150000, 300000, 500000, 2000000]
base_city_quantities = [30, 13, 12, 12, 12, 10, 2]
Então, para simular a existência destes $91$ municípios respeitando as quantidades de municípios estabeleciadas (base_city_quantities) e a aproximação (noise) para o total de habitantes (base_city_sizes) de cada um dos municípios:
- Determina-se o tamanho de cada município (
city_size) a partir de um tamanho base (base_city_size) e de uma variação aleatória (noise) deste tamanho base. - Sorteia-se (
random.choices(...)), de modo aleatório, $k = \textrm{city_size}$ indivíduos da população (population) e, com base nisto, conta-se (np.sum(...)) quantos indivíduos deste município tiveram cancer de rim (kidney_cancer_cases). - Calcula-se a proporção (
kidney_cancer_proportion) e o percentual (kidney_cancer_percent) de casos de cancer de rim do município simulado. - Finalmente, cria-se um data frame (
cities_data_frame) com os $91$ municípios simulados com as suas respectivas informações (tamanho, quantidade de casos de cancer de rim, proporção de casos de cancer de rim, percentual de casos de cancer de rim).
%%time
import random
random.seed(random_seed)
# noise varying randomly between -1 to 1 to simulate variation around the base sizes of the cities
noise = st.uniform(loc=-1, scale=2)
sizes_per_city = []
kidney_cancer_cases_per_city = []
kidney_cancer_proportion_per_city = []
kidney_cancer_percent_per_city = []
for i in range(len(base_city_sizes)):
base_city_size = base_city_sizes[i]
base_city_quantity = base_city_quantities[i]
for _ in range(base_city_quantity):
# calculates information about the simulated city
city_size = base_city_size + int(base_city_size * 0.5 * noise.rvs())
kidney_cancer_cases = np.sum(random.choices(population, k=city_size))
kidney_cancer_proportion = kidney_cancer_cases/float(city_size)
kidney_cancer_percent = kidney_cancer_proportion * 100
# insert information about simulated city into arrays
sizes_per_city.append(city_size)
kidney_cancer_cases_per_city.append(kidney_cancer_cases)
kidney_cancer_proportion_per_city.append(kidney_cancer_proportion)
kidney_cancer_percent_per_city.append(kidney_cancer_percent)
# creates a data frame with all cities and its information
cities_data_frame = pd.DataFrame({
'size': sizes_per_city,
'kidney_cancer_cases': kidney_cancer_cases_per_city,
'kidney_cancer_proportion': kidney_cancer_proportion_per_city,
'kidney_cancer_percent': kidney_cancer_percent_per_city
})
Ao ordenar os $91$ municípios pelo percentual de casos de cancer de rim (kidney_cancer_percent), do menor percentual para o maior percentual, e verificar o decil mais baixo (first_decil_idx) e o decil mais alto (last_decil_idx) do percentual de cancer é possível perceber que:
Tanto os municípios com a menor taxa de cancer de rim quanto os municípios com a maior taxa de cancer de rim são, na verdade, os municípios com o menor número de habitantes (aqueles cujo tamanho são cerca de $5000$ habitantes).
Este fenômeno é explicado pela equação $\sigma_\bar{x} = \frac{s}{\sqrt{n}}$, pois, a variação da média é inversamente proporcional ao tamanho da amostra, de modo que os municípios pequenos exibem uma variação (tanto para baixo quanto para cima) muito maior do que os grandes municípios.
sorted_cities_data_frame = cities_data_frame.sort_values(by=['kidney_cancer_percent'])
quantity_of_cities = len(sorted_cities_data_frame.index)
first_decil_idx = int(quantity_of_cities * 0.1)
sorted_cities_data_frame[:first_decil_idx]
last_decil_idx = quantity_of_cities - int(quantity_of_cities * 0.1)
sorted_cities_data_frame[last_decil_idx:quantity_of_cities]
Este fenômeno se torna mais evidente quando plotamos as taxas de cancer de rim (kidney_cancer_percent) contra o tamanho dos municípios (size) numa escala logarítimica (para facilitar a visualização no eixo $x$).
No gráfico resultante, aparece a típica distribuição bivariada em forma de triângulo: quando a população é pequena (lado esquerdo do gráfico), há grande variação nas taxas de câncer; já, quando a população é grande (lado direito do gráfico), há muito pouca variação.
cities_plot = alt.Chart(cities_data_frame).mark_circle().encode(
alt.X('size:Q', title='log(city_size)', scale=alt.Scale(type='log', base=10, zero=False)),
alt.Y('kidney_cancer_percent:Q', scale=alt.Scale(zero=False))
)
cities_plot
Amostras ao mesmo tempo muito grandes e enviesadas¶
Em tudo que vimos até o momento, tudo nos leva a crer que quanto maior o tamanho da amostra maior a garantia de termos resultados mais consistentes, seja porque:
- A estimativa para o erro padrão (standard error) $SE$ da distribuição amostral (sampling distribution) será confiável (como já foi visto aqui).
- A variação da média é inversamente proporcional ao tamanho da amostra, de modo que amostras pequenas exibem uma variação muito maior do que amostras grandes (como vimos no exemplo do câncer de rim).
Como estamos na era do big data, então, está cada vez mais fácil ter acesso a grandes volumes de dados, ou seja, amostras realmente muito grandes, tão grandes que há pessoas que acreditam que "com uma quantidade grande o suficiente de dados, os números falam por sí só", ou seja, como se não precisássemos mais de modelos estatísticos. Este é o caso do Chris Anderson, o editor chefe da revista Wired, quando publicou o artigo THE END OF THEORY: THE DATA DELUGE MAKES THE SCIENTIFIC METHOD OBSOLETE em que ele cita
"With enough data, the numbers speak for themselves" (Fonte: The End of Theory: The data deluge makes the scientific method obsolete", Chris Anderson, 2008.)
No entanto, existe um conceito em estatística denominado viés estatístico (statistical bias) que não foi levado em consideração na afirmação do Chris Anderson.
"Bias is disproportionate weight in favor of or against one thing, person, or group compared with another, usually in a way considered to be unfair." (Fonte: https://en.wikipedia.org/wiki/Bias)
"A statistic is biased if it is calculated in such a way that it is systematically different from the population parameter being estimated." (Fonte: https://en.wikipedia.org/wiki/Bias_(statistics))
Mas para entendermos na prática os perigos presentes em amostras ao mesmo tempo muito grandes e enviesadas, primeiramente, vamos verificar a definição formal de viés estatístico (statistical bias).
"In statistics, the bias (or bias function) of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. (Fonte: https://en.wikipedia.org/wiki/Bias_of_an_estimator)
Matematicamante, para uma dada estimativa $\hat{\theta}$ de uma quantidade desconhecida $\theta$, temos que:
$$ {Bias}_{\theta} \left[ \hat{\theta} \right] = {E}_{\theta} \left[ \hat{\theta} \right] - \theta $$onde, $\theta$ é o valor real no qual estamos interessados conhecer, $\hat{\theta}$ é uma estimativa para este valor real e ${E}_{\theta} \left[ \hat{\theta} \right]$ é o valor esperado para esta estimativa.
Ou seja, viés (bias) é simplesmente a diferença entre o valor esperado (expected value) para a estimativa $\hat{\theta}$ e o valor real de interesse $\theta$.
Então, podemos realizar uma pequena simulação para ver o que acontece com o viés (bias) na medida em que aumentamos o tamanho das amostras. Para isto, vamos aproveitar um exemplo dado por Christopher Fonnesbeck, no SciPy 2015, em sua palestra entitulada Statistical Thinking for Data Science (que, aliás, eu recomendo que assistam).
Temos abaixo um loop que itera por tamanhos de amostras (sample_sizes) que variam de $10$ a $100.000$. Para cada tamanho $n$ de amostra iremos simular $1.000$ replicações em que:
- Geramos uma amostra aleatória (random sample), representada por
true_sample, de tamanho $n$ a partir da distribuição normal padrão $\text{true_sample} \sim N\left(\mu=0, \sigma=1 \right)$. - Para cada valor presente nesta amostra aleatória (random sample), se o valor é negativo, então, iremos -- com probabilidade $0,5$ -- remover este valor da amostra (ou seja, torná-lo faltante -- missing value).
Em outras palavras, estamos induzindo um viés (bias) no qual valores maiores terão mais chance de serem observados do que valores menores.
%%time
p = 0.5
sample_sizes = [10, 100, 1000, 10000, 100000]
replicates = 1000
biases_df = {'bias': [], 'sample_size': []}
for n in sample_sizes:
for i in range(replicates):
true_sample = np.random.normal(size=n) # standard normal distribution (mean = 0, var = 1)
negative_values = true_sample < 0
missing = np.random.binomial(1, p, n).astype(bool)
observed_sample = true_sample[~(negative_values & missing)]
biases_df['bias'].append(observed_sample.mean())
biases_df['sample_size'].append(n)
%matplotlib inline
import seaborn as sns; sns.set()
sns.set(style='whitegrid')
ax = sns.violinplot(x='sample_size', y='bias', data=biases_df, scale='width', bw=0.5)
ax.set_xlabel("sample size")
ax.set_ylabel("bias")
ax.hlines(y=0, xmin=-0.5, xmax=4.5, color='red')
O resultado da simulação pode ser analisado através do gráfico acima. No eixo $x$ temos os tamanhos de amostras simulados (n), no eixo $y$ a escala para as médias dos valores observados (observed_sample.mean()) e no interior do gráfico uma representação da distribuição das médias dos valores observados para cada tamanho de amosta. A linha vermelha representa a média da distribuição normal padrão (ou seja, o valor $0$).
Então, à medida em que o tamanho da amostra aumenta é possível perceber que o problema fica cada vez pior, ou seja, com amostras grandes, além do viés (bias) não ser eliminado passamos a obter estimativas muito erradas com uma precisão muito alta.
Então, para que coletar muitos dados? Qual é, afinal, a vantagem de trabalhar com big data? Na prática, o viés (bias) é apenas parte da história. Uma das maneiras de medir a acurácia (accuracy) é em termos do erro médio quadrático (mean squared error - MSE) que pode ser matematicamente escrito como:
$$ {MSE} \left( \hat{\theta} \right) = {E} \left[ \left( \hat{\theta} - \theta \right)^2 \right] = {Var} \left( \hat{\theta} \right) + {Bias} \left( \hat{\theta} \right)^2 $$Logo, a acurácia (accuracy) tem duas partes:
- a variância (variance) -- ${Var} \left( \hat{\theta} \right)$ -- que reduz com o aumento do tamanho da amostra, ou seja, aumenta-se a precisão de uma estimativa com o aumento do tamanho da amostra;
- o viés (bias) -- ${Bias} \left( \hat{\theta} \right)^2$ -- que não se modifica com o aumento do tamanho da amostra.
Assim, independentemente de os números poderem falar por si, parece haver um papel para os modelos e, certamente, para os princípios estatísticos dentro da análise de dados. Ou, sendo até mais rigoroso neste aspecto, podemos usar a citação do Nate Silver que diz que "os números não têm como falar por si mesmos".
"Numbers have no way of speaking for themselves" (Fonte: The Signal and the Noise: The Art and Science of Prediction", Nate Silver, 2012.)
Resumo¶
R1. A equação $\sigma_\bar{x} = \frac{s}{\sqrt{n}}$, onde $\sigma_\bar{x}$ é o erro padrão (standard error) da média, releva que:
- A variabilidade ($s$) nos dados aumenta proporcionalmente à raíz quadrada do tamanho da amostra ($\sqrt{n}$), ao invés de proporcionalmente ao tamanho $n$ da amostra (como muitos acreditam que seja o caso).
- A variação ($SE = \sigma_\bar{x}$) da média é inversamente proporcional à raíz quadrada do tamanho da amostra ($\sqrt{n}$), ou seja, amostras pequenas apresentam uma variação muito maior do que amostras muito grandes.
R2. Uma das maneiras de medir a acurácia (accuracy) é em termos do erro médio quadrático (mean squared error - MSE) que pode ser matematicamente escrito como:
$$ {MSE} \left( \hat{\theta} \right) = {E} \left[ \left( \hat{\theta} - \theta \right)^2 \right] = {Var} \left( \hat{\theta} \right) + {Bias} \left( \hat{\theta} \right)^2 $$Logo, a acurácia (accuracy) é composta por partes:
- a variância (variance) -- ${Var} \left( \hat{\theta} \right)$ -- que reduz com o aumento do tamanho da amostra, ou seja, aumenta-se a precisão de uma estimativa com o aumento do tamanho da amostra;
- o viés (bias) -- ${Bias} \left( \hat{\theta} \right)^2$ -- que não se modifica com o aumento do tamanho da amostra.
Referências:
- http://www-stat.wharton.upenn.edu/~hwainer/Readings/Most%20Dangerous%20eqn.pdf
- https://en.wikipedia.org/wiki/Guinea_(coin)
- https://en.wikipedia.org/wiki/Bernoulli_distribution
- https://www.wired.com/2008/06/pb-theory/
- https://en.wikipedia.org/wiki/Bias
- https://en.wikipedia.org/wiki/Bias_(statistics)
- https://en.wikipedia.org/wiki/Bias_of_an_estimator
- https://www.youtube.com/watch?v=TGGGDpb04Yc
- https://en.wikipedia.org/wiki/Mean_squared_error