O Teorema Central do Limite¶
Primeiramente, vamos passar por alguns conceitos.
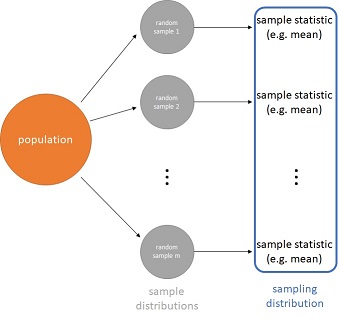
Suponha que há uma população (population) de interesse e que foi coletada uma amostra aleatória (random sample) da mesma. Suponha também que a partir desta amostra (sample) foi calculada alguma estatística desta amostra (sample statistic), por exemplo, a média (mean) desta amostra (sample).
Suponha que uma outra amostra aleatória (random sample) seja coletada e que a sua média (mean) seja também calculada e armazenada, e que este mesmo processo se repita muitas vezes.
Cada uma destas amostras aleatórias (random samples) terá a sua própria distribuição, que é denominada distribuição da amostra (sample distribution). Cada observação pertencente a uma destas distribuições é uma unidade amostrada aleatoriamente (randomly sampled unit) da população (population); digamos, uma pessoa, um gato ou um cachorro dependendo de qual é a população (population) a ser estudada.
Além disto, os valores que foram calculados e armazenados, as estatísticas das amostras (sample statistics), também formam uma nova distribuição. No entanto, nesta nova distribuição, cada observação da mesma não é mais uma unidade da população (population), mas sim uma estatística desta amostra (sample statistic), no nosso exemplo, a média da amostra (sample mean). A distribuição destas estatísticas das amostras (sample statistics) é denominada distribuição amostral (sampling distribution).
Logo, os dois termos distribuição da amostra (sample distribution) e distribuição amostral (sampling distribution) parecem similares, porém, representam conceitos diferentes.
 (Inspiração: [Inferential Statistics](https://www.coursera.org/learn/inferential-statistics-intro/home/welcome), by Duke University, at Coursera)
(Inspiração: [Inferential Statistics](https://www.coursera.org/learn/inferential-statistics-intro/home/welcome), by Duke University, at Coursera)
Geralmente, não temos acesso à população (population) e, portanto, nem aos seus parâmetros (por exemplo, a média da população $\mu$). Na prática, temos acesso a amostras aleatórias (random samples) desta população (population).
Então, para estimar o valor de um parâmetro da população (population) utilizamos uma estatística da amostra (sample statistic) como se fosse uma estimativa pontual (point estimate) para o parâmetro da população (population). Como exemplo, a média da amostra (sample mean) é utilizada para estimar a média da população (population mean).
No entanto, estas estimativas pontuais (point estimates) irão variar de uma amostra aleatória (random sample) para outra. Esta variabilidade é a variabilidade amostral (sampling variability), também conhecida como erro padrão (standard error) $SE$.
Então, o Teorema Central do Limite (Central Limit Theorem - CLT) estabelece que quando o tamanho das amostras (samples) é suficientemente grande, a distribuição das estatísticas das amostras (sample statistics) é aproximadamente normal (nearly normal) sendo que quando a estatística da amostra (sample statistic) é a média, então, esta distribuição é centrada na média da população (population mean) e com um desvio padrão (standard deviation) igual ao desvio padrão da população (population standard deviation) dividido pela raiz quadrada do tamanho das amostras (samples size).
$$ \bar{X} \sim N\left(mean=\mu, SE=\frac{\sigma}{\sqrt{n}}\right) $$As condições para que o Teorema Central do Limite (Central Limit Theorem - CLT) seja válido são:
- Independência (Independence): as unidades amostradas aleatoriamente (randomly sampled units) devem ser independentes, ou seja, a ocorrência de uma dada unidade amostrada (sampled unit) da população (population) não afeta a probabilidade da ocorrência de outra.
- Tamanho da Amostra/Amostra Enviesada (Sample Size/Skewed): ou a distribuição da população (population) é normal, ou se a distribuição da população (population) é enviesada (skewed), o tamanho da amostra (sample size) tem que ser grande (regra de ouro: $n > 30$).
Repare que, respeitadas as condições, o Teorema Central do Limite (Central Limit Theorem - CLT) aplica-se independentemente da forma da distribuição da população (population), ou seja, mesmo que a população (population) não tenha uma distribuição normal, a distribuição amostral (sampling distribution) das estatísticas das amostras (sample statistics) será aproximadamente normal (nearly normal).
Muitos procedimentos estatísticos comuns requerem que os dados sejam aproximadamente normais, daí a importância do Teorema Central do Limite (Central Limit Theorem - CLT).
Então, vamos verificar na prática a realização do Teorema Central do Limite (Central Limit Theorem - CLT) através de algumas simulações simples.
Primeiramente, vamos importar alguns pacotes.
from scipy import stats as st
import pandas as pd
import numpy as np
# Import some dependencies to visualization with altair
import altair as alt
alt.renderers.enable('notebook') # for the notebook only (not for JupyterLab) run this command once per session
Na nossa simulação, vamos testar como o Teorema Central do Limite (Central Limit Theorem - CLT) se comporta para $3$ tamanhos diferentes de amostras (samples), no caso: $10$, $30$ e $500$. Além disto, vamos coletar $5.000$ amostras (samples) da população (population) de interesse, ou seja, o tamanho da distribuição amostral (sampling distribution) das estatísticas das amostras (sample statistics) será igual a $5.000$.
random_sample_size1 = 10
random_sample_size2 = 30
random_sample_size3 = 500
sampling_distribution_size = 5000
Então, a nossa simulação consiste em:
- Escolher uma distribuição para representar a população (population) de interesse.
- Coletar, aleatoriamente, $n$ valores a partir desta distribuição (distribution) e calcular a média (mean) destes valores (aqui, já sabemos que experimentaremos com $3$ valores diferentes de $n$: $10$, $30$ e $500$).
- Repetir os passos anteriores $m$ vezes obtendo $m$ médias (means). Aqui, já sabemos que $m = 5.000$ (
sampling_distribution_size). - Finalmente:
- Plotar a curva que representa a distribuição (distribution) teórica selecionada no passo $1$.
- Plotar o histograma das $m$ médias (means), ou seja, plotar a distribuição amostral (sampling distribution) das estatísticas das amostras (sample statistics).
- Verificar se o histograma da distribuição amostral (histogram of the sampling distribution) tem um formato que se aproxima de uma distribuição normal independentemente da distribuição (distribution) teórica selecionada no passo $1$.
- Verificar se a média da distribuição amostral (sampling distribution) é uma boa aproximação para a média da distribuição da população (population distribution).
- Verificar se o desvio padrão (standard deviation) da distribuição amostral (sampling distribution) é uma boa aproximação para $\frac{\sigma}{\sqrt{n}}$.
As funções abaixo são funções utilitárias para plotar os gráficos e nos ajudar a verificar os itens A, B e C.
def draw_hist_plot(sampling_distribution, sampling_distribution_size, random_sample_size, x_axis_limits=None):
sampling_distribution_mean = np.mean(sampling_distribution)
sampling_distribution_sd = np.std(sampling_distribution)
title = 'Sampling Dist. (m={0}, n={1}) of Means | mean={2:.2f} se={3:.2f}'.format(
sampling_distribution_size, random_sample_size, sampling_distribution_mean, sampling_distribution_sd
)
data = pd.DataFrame({'means': sampling_distribution})
hist = None
if x_axis_limits is None:
hist = alt.Chart(data).mark_bar().encode(
alt.X('means', bin=True),
alt.Y('count()')
).properties(title=title)
else:
hist = alt.Chart(data).mark_bar().encode(
alt.X('means', bin=True, scale=alt.Scale(domain=x_axis_limits)),
alt.Y('count()')
).properties(title=title)
rule = alt.Chart(data).mark_rule(color='red').encode(
x='mean(means)',
size=alt.value(2)
)
return hist + rule
def draw_density_plot(pop_distribution, distribution_name):
# Create the points to draw the probability density function
x_i = pop_distribution.ppf(0.001)
x_f = pop_distribution.ppf(0.999)
x = np.linspace(x_i, x_f, 100)
f_x = pop_distribution.pdf(x)
# draw the density function f(x)
data = pd.DataFrame({'x': x, 'f(x)': f_x})
density = alt.Chart(data).mark_line().encode(
x='x',
y='f(x)'
).properties(title='Population = {0}'.format(distribution_name))
return density
def draw_plots(pop_distribution, distribution_name, sampling_distribution1, sampling_distribution2, sampling_distribution3):
density_plot = draw_density_plot(pop_distribution, distribution_name)
x_axis_limits = (np.min(sampling_distribution1), np.max(sampling_distribution1))
hist1_plot = draw_hist_plot(sampling_distribution1, sampling_distribution_size, random_sample_size1)
hist2_plot = draw_hist_plot(sampling_distribution2, sampling_distribution_size, random_sample_size2, x_axis_limits)
hist3_plot = draw_hist_plot(sampling_distribution3, sampling_distribution_size, random_sample_size3, x_axis_limits)
row1_plot = density_plot | hist1_plot
row2_plot = (hist2_plot | hist3_plot).resolve_scale(x='shared')
return alt.vconcat(row1_plot, row2_plot)
A função abaixo é uma função utilitária para nos ajudar a verificar os itens D e E.
def print_pop_stdv_and_bestguess_stdv(pop_distribution, sampling_distribution1, sampling_distribution2,
sampling_distribution3):
pop_standard_deviation = np.sqrt(pop_distribution.stats(moments='v'))
standard_error_sampling_dist1 = np.std(sampling_distribution1)
standard_error_sampling_dist2 = np.std(sampling_distribution2)
standard_error_sampling_dist3 = np.std(sampling_distribution3)
best_guess1_pop_stdv = standard_error_sampling_dist1*np.sqrt(random_sample_size1)
best_guess2_pop_stdv = standard_error_sampling_dist2*np.sqrt(random_sample_size2)
best_guess3_pop_stdv = standard_error_sampling_dist3*np.sqrt(random_sample_size3)
print("Population standard deviation (pop_stdv) = {0} ~ {1:.1f}".format(
pop_standard_deviation, pop_standard_deviation
))
print("Best guess for pop_stdv from a sampling distribution (m={0}, n={1}) = {2} ~ {3:.1f}".format(
sampling_distribution_size, random_sample_size1, best_guess1_pop_stdv, best_guess1_pop_stdv
))
print("Best guess for pop_stdv from a sampling distribution (m={0}, n={1}) = {2} ~ {3:.1f}".format(
sampling_distribution_size, random_sample_size2, best_guess2_pop_stdv, best_guess2_pop_stdv
))
print("Best guess for pop_stdv from a sampling distribution (m={0}, n={1}) = {2} ~ {3:.1f}\n".format(
sampling_distribution_size, random_sample_size3, best_guess3_pop_stdv, best_guess3_pop_stdv
))
Finalmente, a função abaixo é a função que irá executar as replicações da simulação para criar uma distribuição amostral (sampling distribution) para cada um dos $3$ tamanhos diferentes de amostras (samples) que iremos simular.
def make_sampling_distributions(pop_distribution):
sampling_distribution_of_means1 = []
sampling_distribution_of_means2 = []
sampling_distribution_of_means3 = []
for _ in range(sampling_distribution_size):
random_sample = pop_distribution.rvs(size=random_sample_size1)
sample_statistic = random_sample.mean()
sampling_distribution_of_means1.append(sample_statistic)
random_sample = pop_distribution.rvs(size=random_sample_size2)
sample_statistic = random_sample.mean()
sampling_distribution_of_means2.append(sample_statistic)
random_sample = pop_distribution.rvs(size=random_sample_size3)
sample_statistic = random_sample.mean()
sampling_distribution_of_means3.append(sample_statistic)
return sampling_distribution_of_means1, sampling_distribution_of_means2, sampling_distribution_of_means3
As seções subsequentes realizam o mesmo experimento para diferentes distribuições (distributions) teóricas.
Experimento que considera uma população com distribuição Normal¶
%%time
# Definition of the population distribution
pop_par_mu = 0
pop_par_sd = 1
pop_distribution = st.norm(loc=pop_par_mu, scale=pop_par_sd)
pop_distribution_name = "Normal(mean={0},sd={1})".format(pop_par_mu,pop_par_sd)
# Making the sampling distributions of the means
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3 = make_sampling_distributions(pop_distribution)
# Check if the standard error of the sampling distribution approximates from stdv(pop)/sqrt(n)
print_pop_stdv_and_bestguess_stdv(
pop_distribution, sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
# Draw plot of the density function that represents the population distribution
# and histogram of sampling distributions
draw_plots(
pop_distribution, pop_distribution_name,
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
Experimento que considera uma população com distribuição Uniforme¶
https://en.wikipedia.org/wiki/Uniform_distribution_(continuous)
%%time
# Definition of the population distribution
pop_par_a = 1
pop_par_b = 10
pop_distribution = st.uniform(loc=pop_par_a, scale=(pop_par_b-pop_par_a))
pop_mean, pop_var = pop_distribution.stats(moments='mv')
pop_distribution_name = "Uniform(a={0},b={1}) with mean={2}, std={3:.1f}".format(
pop_par_a, pop_par_b, pop_mean, np.sqrt(pop_var)
)
# Making the sampling distributions of the means
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3 = make_sampling_distributions(pop_distribution)
# Check if the standard error of the sampling distribution approximates from stdv(pop)/sqrt(n)
print_pop_stdv_and_bestguess_stdv(
pop_distribution, sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
# Draw plot of the density function that represents the population distribution
# and histogram of sampling distributions
draw_plots(
pop_distribution, pop_distribution_name,
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
Experimento que considera uma população com distribuição Exponencial¶
%%time
# Definition of the population distribution
pop_par_lambda = 1.5
pop_distribution = st.expon(scale=(1 / pop_par_lambda))
pop_mean, pop_var = pop_distribution.stats(moments='mv')
pop_distribution_name = "Exponential(lambda={0}) with mean={1:.2f}, std={2:.1f}".format(
pop_par_lambda, pop_mean, np.sqrt(pop_var)
)
# Making the sampling distributions of the means
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3 = make_sampling_distributions(pop_distribution)
# Check if the standard error of the sampling distribution approximates from stdv(pop)/sqrt(n)
print_pop_stdv_and_bestguess_stdv(
pop_distribution, sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
# Draw plot of the density function that represents the population distribution
# and histogram of sampling distributions
draw_plots(
pop_distribution, pop_distribution_name,
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
Experimento que considera uma população com distribuição Gama¶
%%time
# Definition of the population distribution
pop_par_shape = 2.0
pop_par_scale = 2.0
pop_distribution = st.gamma(a=pop_par_shape, scale=pop_par_scale)
pop_mean, pop_var = pop_distribution.stats(moments='mv')
pop_distribution_name = "Gamma(shape={0},scale={1}) with mean={2:.2f}, std={3:.1f}".format(
pop_par_shape, pop_par_scale, pop_mean, np.sqrt(pop_var)
)
# Making the sampling distributions of the means
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3 = make_sampling_distributions(pop_distribution)
# Check if the standard error of the sampling distribution approximates from stdv(pop)/sqrt(n)
print_pop_stdv_and_bestguess_stdv(
pop_distribution, sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
# Draw plot of the density function that represents the population distribution
# and histogram of sampling distributions
draw_plots(
pop_distribution, pop_distribution_name,
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
Experimento que considera uma população com distribuição Log-Normal (variância infinita)¶
%%time
# Definition of the population distribution
pop_par_mu = np.exp(0)
pop_par_sd = 1.5 # example of heavy tail
pop_distribution = st.lognorm(s=pop_par_sd, loc=0, scale=pop_par_mu)
pop_distribution_name = "Log-Normal(mean={0},sd={1})".format(pop_par_mu, pop_par_sd)
# Making the sampling distributions of the means
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3 = make_sampling_distributions(pop_distribution)
# Check if the standard error of the sampling distribution approximates from stdv(pop)/sqrt(n)
print_pop_stdv_and_bestguess_stdv(
pop_distribution, sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
# Draw plot of the density function that represents the population distribution
# and histogram of sampling distributions
draw_plots(
pop_distribution, pop_distribution_name,
sampling_dist_of_means1, sampling_dist_of_means2, sampling_dist_of_means3
)
Neste caso específico em que a população (population) é representada por uma distribuição Log-Normal é possível observar que:
- os histogramas das distribuições amostrais (sampling distributions) não se aproximam de uma normal;
- a média das distribuições amostrais (sampling distributions) não são boas aproximações para a médida da população (population).
Como pode ser visto na Wikipedia:
In more general usage, a central limit theorem is any of a set of weak-convergence theorems in probability theory. They all express the fact that a sum of many independent and identically distributed ($i.i.d.$) random variables, or alternatively, random variables with specific types of dependence, will tend to be distributed according to one of a small set of attractor distributions. When the variance of the $i.i.d.$ variables is finite, the attractor distribution is the normal distribution. In contrast, the sum of a number of $i.i.d.$ random variables with power law tail distributions decreasing as $|x|^{−\alpha −1}$ where $0 < \alpha < 2$ (and therefore having infinite variance) will tend to an alpha-stable distribution with stability parameter (or index of stability) of $\alpha$ as the number of variables grows. (Fonte: https://en.wikipedia.org/wiki/Central_limit_theorem)
Em outras palavras, uma vez que a distribuição Log-Normal utilizada no exemplo anterior
$$ \textrm{population} = \textrm{Log-Normal}\left(\mu=1,\sigma=1.5 \right) $$tem uma variância (variance) infinita (ou seja, tem uma cauda muito longa - heavy tail), então, a distribuição amostral (sampling distribution) resultante não será Normal.
Resumo¶
R1. Uma estatística da amostra (sample statistic) é uma estimativa pontual (point estimate) para um parâmetro da população (population), por exemplo, a média da amostra (sample mean) é utilizada para estimar a média da população (population mean). Os termos estatística da amostra (sample statistic) e estimativa pontual (point estimate) são sinônimos.
R2. Estimativas pontuais (point estimates) variam de uma amostra (sample) para outra. Esta variabilidade é a variabilidade amostral (sampling variability), também conhecida como erro padrão (standard error) $SE$.
R3. A variabilidade amostral (sampling variability) da média, ou seja o erro padrão (standard error) $SE$ da média, é calculada como $SE=\frac{\sigma}{\sqrt{n}}$, onde $\sigma$ é o desvio padrão (standard deviation) da população (population).
- Quando o desvio padrão (standard deviation) $\sigma$ da população (population) não é conhecido (quase sempre), então, o erro padrão (standard error) $SE$ pode ser estimado através do desvio padrão (standard deviation) da amostra (sample) $s$, de forma que $SE \approx \hat{se}=\frac{s}{\sqrt{n}}$.
R4. O Teorema Central do Limite (Central Limit Theorem - CLT) diz respeito à distribuição das estatísticas das amostras (sample statistics) e, sob certas condições, esta distribuição será aproximadamente normal (nearly normal).
Quando a estatística da amostra (sample statistic) é a média, então, o Teorema Central do Limite (Central Limit Theorem - CLT) estabelece que se:
- (1a) o tamanho da amostra (sample size) é suficientemente grande ($n > 30$ ou maior se os dados são consideravelmente enviesados), ou
- (1b) sabe-se de antemão que a população (population) tem uma distribuição normal, e
- (2) as observações da amostra (sample) são independentes,
então a distribuição das médias das amostras (samples) será aproximadamente normal (nearly normal), centrada na média da população (population mean) $\mu$ e com um erro padrão (standard error) de $SE=\frac{\sigma}{\sqrt{n}}$:
$$ \bar{X} \sim N\left(mean=\mu, SE=\frac{\sigma}{\sqrt{n}}\right) $$