< Intervalo de Confiança, Margem de Erro, Acurácia e Precisão | Conteúdo | Tamanho da Amostra, Variância e Viés >

Open in Colab

Para que serve uma amostra de tamanho grande?

Uma vez que as observações são independentes (independents) e a distribuição da população (population) destas observações não é muito enviesada (skewed), então, o fato de termos amostras aleatórias (random samples) grandes garante que:

  1. Teremos uma distribuição amostral (sampling distribution) da média que é aproximadamente Normal (como já foi visto aqui);
  2. A estimativa para o erro padrão (standard error) $SE$ desta distribuição amostral (sampling distribution) será confiável.

Então, para verificarmos o ponto 2, considere que a distribuição da população (population) seja dada por

$$ \textrm{pop} \sim N \left( \mu=0, \sigma=1 \right) $$

ou seja, uma população (population) com média $\mu = 0$ e desvio padrão $\sigma = 1$.

In [1]:
from scipy import stats as st

# Definition of the population distribution
pop_par_mu = 0
pop_par_sd = 1
pop_distribution = st.norm(loc=pop_par_mu, scale=pop_par_sd)

Considere que iremos coletar $m$ amostras aleatórias (random samples) desta população (population) onde $m=$ sampling_distribution_size. Considere também que cada uma destas $m$ amostras aleatórias (random samples) tenha um tamanho $n$, onde $n=$ random_sample_size.

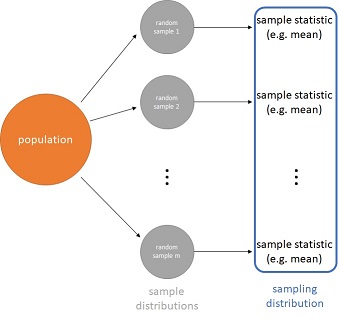pop-sample-sampling (Inspiração: [Inferential Statistics](https://www.coursera.org/learn/inferential-statistics-intro/home/welcome), by Duke University, at Coursera)

Se calcularmos a média de cada uma destas $m$ amostras aleatórias (random samples), então, teremos uma distribuição amostral (sampling distribution) das médias, denotada no código por sampling_distribution_of_means.

A partir da distribuição amostral (sampling distribution) das médias nós podemos:

  1. Estimar um valor $\hat{\mu}$ (estimated_mean) para a média $\mu$ da população (population);
  2. Estimar o grau de precisão $SE$ (standard_error_sampling_dist) com o qual este valor estimado $\hat{\mu}$ (estimated_mean) representa a média $\mu$ da população (population).

Esta estimativa do grau de precisão é dada pelo erro padrão (standard error), cuja definição pela wikidepia é a seguinte:

The standard error (SE) of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the parameter or the statistic is the mean, it is called the standard error of the mean (SEM) (Fonte: https://en.wikipedia.org/wiki/Standard_error)

Primeiramente, o que queremos verificar aqui é se a precisão dada pelo erro padrão (standard error) aumenta na medida em que o tamanho $n$ das amostras aleatórias (random samples) também aumenta.

In [2]:
import numpy as np

random_sample_sizes = [10, 30, 100, 500, 1000, 5000, 10000, 50000, 100000]
sampling_distribution_size = 1000
estimated_means = []
standard_errors = []
for random_sample_size in random_sample_sizes:
    sampling_distribution_of_means = []
    for _ in range(sampling_distribution_size):
        random_sample = pop_distribution.rvs(size=random_sample_size)
        sampling_distribution_of_means.append(np.mean(random_sample))

    estimated_mean = np.mean(sampling_distribution_of_means)
    estimated_means.append(estimated_mean)
    
    standard_error_sampling_dist = np.std(sampling_distribution_of_means)
    standard_errors.append(standard_error_sampling_dist)
In [3]:
import pandas as pd
import altair as alt
alt.renderers.enable('notebook') # for the notebook only (not for JupyterLab) run this command once per session

def plot_truemean_estimatedmean_ME(true_mean, estimated_means, estimated_standard_errors, random_sample_sizes):
    data = pd.DataFrame({
        'true_mean': true_mean, 'random_sample_size': random_sample_sizes, 
        'estimated_mean': estimated_means, 'estimated_se': estimated_standard_errors
    })
    
    true_mean_plot = alt.Chart(data).mark_rule(color='red').encode(
        y='true_mean:Q',
        size=alt.value(1)
    )
    
    estimated_mean_plot = alt.Chart(data).mark_line().encode(
        x='random_sample_size:O',
        y='estimated_mean'
    )
    
    margin_of_error_plot = alt.Chart(data).mark_area(opacity=0.3).encode(
        x='random_sample_size:O',
        y='mu_hat_sup:Q',
        y2='mu_hat_inf:Q'
    ).transform_calculate(
        mu_hat_sup='datum.estimated_mean + (1.96*datum.estimated_se)',
        mu_hat_inf='datum.estimated_mean - (1.96*datum.estimated_se)',
    )
    
    chart1 = (estimated_mean_plot + margin_of_error_plot).properties(title='Estimated Mean +- 1.96*SE')
    chart2 = (true_mean_plot + margin_of_error_plot).properties(title='True mean (in red)')
    chart3 = (true_mean_plot + estimated_mean_plot).properties(title='True (red) and Estimated (blue) means')
    
    return chart1 | chart2 | chart3
In [4]:
plot_truemean_estimatedmean_ME(pop_par_mu, estimated_means, standard_errors, random_sample_sizes)
Out[4]:










    




























Os gráficos acima, da esquerda para a direita, representam:


    

  • Esquerda:
      

    • curva azul representando as estimativas ($\hat{\mu}$) para a média $\mu$ da população (population) para cada um dos tamanhos $n$ (random_sample_size) que foram simulados;
      • 

    • área azul representando o intervalo de confiança de $95\%$ ($\hat{\mu} \pm 1.96 \times SE$) das estimativas $\hat{\mu}$.
      • 

    

    • 

  • Centro:
      

    • curva vermelha representando a média $\mu$ da população (population);
      • 

    • área azul idem ao gráfico da esquerda.
      • 

    

    • 

  • Direita:
      

    • curva vermelha idem ao gráfico do meio;
      • 

    • curva azul idem ao gráfico da esquerda;
      • 

    

    • 





Logo, é possível perceber que na medida em que o tamanho $n$ (`random_sample_size`) das amostras aleatórias (random samples) aumenta, o grau de precisão $SE$ da estimativa $\hat{\mu}$ também aumenta (ou seja, a margem de erro reduz, reduzindo também a largura do intervalo de confiança).




Além disto, pelo Teorema Central do Limite (Central Limit Theorem - CLT) temos que: a distribuição de médias de uma amostra é aproximadamente normal (nearly normal), centrada na média $\mu$ da população (population), e com um desvio padrão (standard deviation) igual ao desvio padrão (standard deviation) da população (population) dividido pela raiz quadrada do tamanho $n$ da amostra.

$$
\bar{X} \sim N\left(mean=\mu, SE=\frac{\sigma}{\sqrt{n}}\right)
$$
No entanto, nem sempre temos o desvio padrão (standard deviation) $\sigma$ da população (population). Nestes casos, tipicamente, o desvio padrão (standard deviation) $\sigma$ da população (population) é estimado como sendo o desvio padrão $s$ (standard deviation) da amostra aleatória (random sample) em questão. Então, uma estimativa para o erro padrão (standard error) da distribuição amostral (sampling distribution) a partir de uma amostra aleatória (random sample) de tamanho $n$ é dada por:

$$
\hat{se} = \frac{s}{\sqrt{n}}
$$
O que queremos verificar aqui é se esta estimativa $\hat{se}$ para o erro padrão (standard error) fica mais precisa na medida em que o tamanho $n$ das amostras aleatórias (random samples) aumenta.













In [5]:



    


def estimate_SEs(pop_distribution, random_sample_sizes):
    estimated_standard_errors = []
    for random_sample_size in random_sample_sizes:
        random_sample = pop_distribution.rvs(size=random_sample_size)
        estimated_standard_error = np.std(random_sample) / np.sqrt(random_sample_size)
        estimated_standard_errors.append(estimated_standard_error)
    return estimated_standard_errors

estimated_standard_errors1 = estimate_SEs(pop_distribution, random_sample_sizes)
estimated_standard_errors2 = estimate_SEs(pop_distribution, random_sample_sizes)
estimated_standard_errors3 = estimate_SEs(pop_distribution, random_sample_sizes)



    













In [6]:



    


def plot_true_and_estimated_standarderror(standard_errors, estimated_standard_errors, random_sample_sizes):
    data = pd.DataFrame({
        'SE': standard_errors,
        'estimated_SE': estimated_standard_errors,
        'random_sample_size': random_sample_sizes, 
    })
    
    SE_plot = alt.Chart(data).mark_line(color='red', opacity=1).encode(
        x='random_sample_size:O',
        y='SE:Q'
    )
    
    estimated_SE_plot = alt.Chart(data).mark_line(opacity=1).encode(
        x='random_sample_size:O',
        y='estimated_SE:Q'
    )
    
    return SE_plot + estimated_SE_plot



    













In [7]:



    


chart1 = plot_true_and_estimated_standarderror(standard_errors, estimated_standard_errors1, random_sample_sizes)
chart2 = plot_true_and_estimated_standarderror(standard_errors, estimated_standard_errors2, random_sample_sizes)
chart3 = plot_true_and_estimated_standarderror(standard_errors, estimated_standard_errors3, random_sample_sizes)

chart = (chart1 | chart2 | chart3).resolve_scale(y='shared')
chart



    















    




















    
Out[7]:


















    




























Os gráficos acima representam 3 comparações entre o erro padrão $SE$ (standard error) da distribuição amostral (sampling distribution) e a estimativa $\hat{se}$ deste erro padrão $SE$ (standard error). A curva azul representa a estimativa $\hat{se}$ por tamanho de amostra ($n$) enquanto que a curva vermelha representa o $SE$.




Logo, é possível perceber que na medida em que o tamanho $n$ (`random_sample_size`) das amostras aleatórias (random samples) aumenta, a estimativa $\hat{se}$ se aproxima do valor de $SE$.

















Resumo
R1. Na medida em que o tamanho $n$ (random_sample_size) das amostras aleatórias (random samples) aumenta:


    

  • a estimativa $\hat{\mu}$ para a média da população (population) se aproxima do valor real $\mu$;
    • 

  • a estimativa $\hat{se}=\frac{s}{\sqrt{n}}$ para o erro padrão (standard error) da estimativa da média se aproxima do valor de $SE=\frac{\sigma}{\sqrt{n}}$;
    • 

  • o grau de precisão $SE$ da estimativa $\hat{\mu}$ também aumenta (ou seja, a margem de erro reduz, reduzindo também a largura do intervalo de confiança).
    • 
















Referências:

















< Intervalo de Confiança, Margem de Erro, Acurácia e Precisão | Conteúdo | Tamanho da Amostra, Variância e Viés >


Open in Colab













In [ ]: