< Tamanho da Amostra, Variância e Viés | Conteúdo | [A ser definido] >
Teste de Hipótese, o início¶
Já vimos aqui que um dos problemas clássicos da estatística consiste em estimar o valor de um parâmetro desconhecido, por exemplo, estimar a média $\mu$ de uma população (population) a partir:
- (1a) de uma amostra aleatória (random sample) $x = \{ x_1, x_2, \ldots, x_n \}$ desta população (population) e
- (1b) de um estimador (estimator) para a média, ou seja, um algoritmo como a média aritmética $\bar{x} = \sum_{i=1}^n \frac{x_i}{n}$;
- (2) além de se basear no Teorema Central do Limite (Central Limit Theorem - CLT) e nas suas condições para fornecermos uma inferência a respeito da precisão do algoritmo (média aritmética) através do cálculo da aproximação $\hat{se}$ para o erro padrão (standard error) $SE$ desta estimativa via $SE \approx \hat{se} = \frac{s}{\sqrt{n}}$.
Um outro problema muito comum na estatística clássica é verificar se uma dada hipótese é plausível em detrimento de outra com base nos dados observados. Considere o seguinte exemplo:
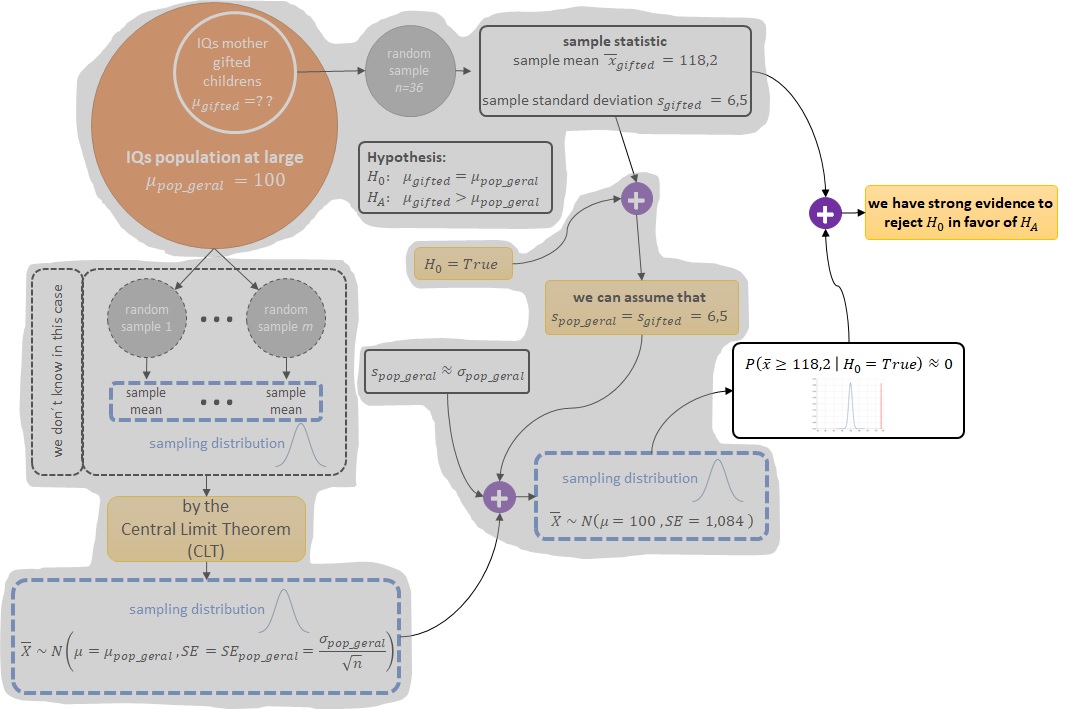
Researchers investigating characteristics of gifted children collected data from schools in a large city on a random sample of $36$ children who were identified as gifted children soon after they reached the age of four. In this study, along with variables on the children, the researchers also collected data on the mother's IQ of the $36$ randomly sampled gifted children. Our goal is to evaluate if these data provide convincing evidence that the average IQ of mothers of gifted children is different than the average IQ for the population at large, which is $100$. (Fonte: "A. Graybill and H.K. Iyer. Regression Analysis: Concepts and Applications. Duxbury Press, 1994, pp. 511-516") (Fonte: https://www.openintro.org/stat/textbook.php?stat_book=os)
import pandas as pd
gifted_df = pd.read_csv("data/gifted.txt", delimiter='\t')
gifted_df.head()
# some statistics about the IQ of mothers of gifted children from this random sample
gifted_df.motheriq.describe()
import matplotlib.pyplot as plt
%matplotlib inline
# histogram of IQ of mothers of gifted children from this random sample
gifted_df.hist(column='motheriq', bins=(100,105,110,115,120,125,130,135))
A população (population) em foco aqui consiste nas mães de crianças superdotadas e o parâmetro de interesse é o QI médio das mães de crianças superdotadas. Além disto, observou-se um QI médio $\bar{x}_{gifted} = 118,2$ de uma amostra aleatória (random sample) de $n = 36$ mães de crianças superdotadas.
n = len(gifted_df.index)
mean_observed_IQ_gifted = gifted_df.motheriq.mean()
print("Random sample size = {0}".format(n))
print("Observed average IQ of mothers of gifted children = {0:.1f}".format(mean_observed_IQ_gifted))
Queremos verificar se estes dados observados suportam a hipótese ($H_A$) de que o QI médio das mães de crianças superdotadas ($\mu_{gifted}$, que é desconhecido) é maior do que o QI médio para a população geral (que é igual a $\mu_{pop\_geral} = 100$) versus a outra hipótese ($H_0$) de que o QI médio das mães de crianças superdotadas não é tão diferente assim do QI médio para a população geral. Ou seja:
- $H_0$: o QI médio das mães de crianças superdotadas não é diferente do QI médio para a população geral, ou seja, $\mu_{gifted} = \mu_{pop\_geral}$.
- $H_A$: o QI médio das mães de crianças superdotadas é maior do que o QI médio para a população geral, ou seja, $\mu_{gifted} \gt \mu_{pop\_geral}$.
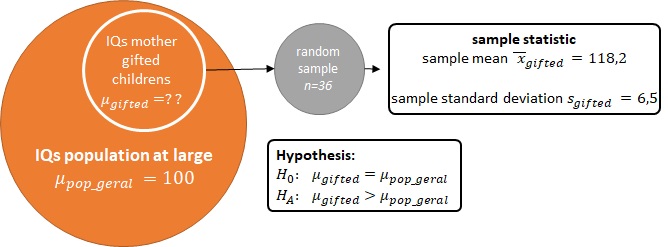
Em outras palavras, será que este QI médio $\bar{x}_{gifted}=118,2$ observado é raro o suficiente dentro dos valores de QIs médios da população geral para que possamos considerar o QI médio das mães de crianças superdotadas como diferente do QI médio para a população geral (que é igual a $\mu_{pop\_geral}=100$)?
Até aqui estamos o tempo todo nos referindo ao QI médio, ou seja, estamos nos referindo a uma estatística da amostra (sample statistic) que no nosso caso é a média da amostra (sample mean). E, como já vimos aqui, a distribuição destas estatísticas das amostras (sample statistics) é denominada distribuição amostral (sampling distribution).
Então, novamente em outras palavras, se tivermos a distribuição amostral (sampling distribution) das médias de QIs para a população geral:
- $H_A$: A probabilidade de uma média de QI igual ou mais extrema do que $118,2$ é pequena o suficiente para considerarmos raro o evento de termos observado, na prática, um QI médio $\bar{x}_{gifted}=118,2$?
- $H_0$: Ou será que esta probabilidade não é tão pequena, indicando que um QI médio de $\bar{x}_{gifted}=118,2$ não é tão diferente do QI médio da população geral $\mu_{pop\_geral}=100$?
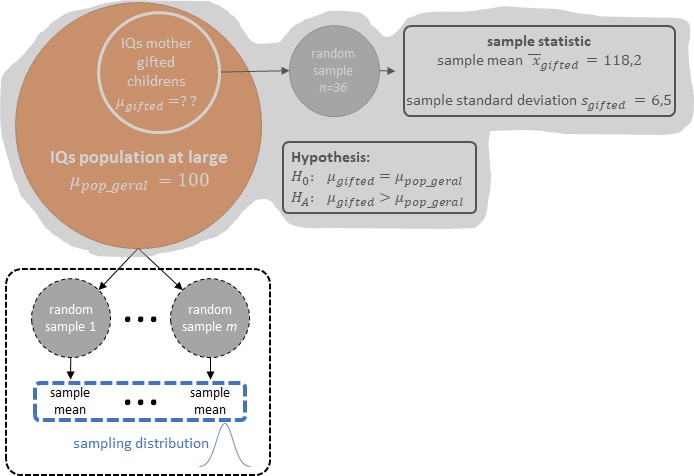
E por falar em distribuição amostral (sampling distribution), podemos invocar aqui o Teorema Central do Limite (Central Limit Theorem - CLT) que nos diz que quando a estatística da amostra (sample statistic) é a média, se:
- (1a) o tamanho da amostra (sample size) é suficientemente grande ($n > 30$ ou maior se os dados são consideravelmente enviesados), ou
- (1b) sabe-se de antemão que a população (population) tem uma distribuição normal, e
- (2) as observações da amostra (sample) são independentes,
então, a distribuição das médias das amostras (samples) será aproximadamente normal (nearly normal), centrada na média da população (population mean) $\mu$ e com um erro padrão (standard error) de $SE=\frac{\sigma}{\sqrt{n}}$:
$$ \bar{X} \sim N\left(mean=\mu, SE=\frac{\sigma}{\sqrt{n}}\right) $$
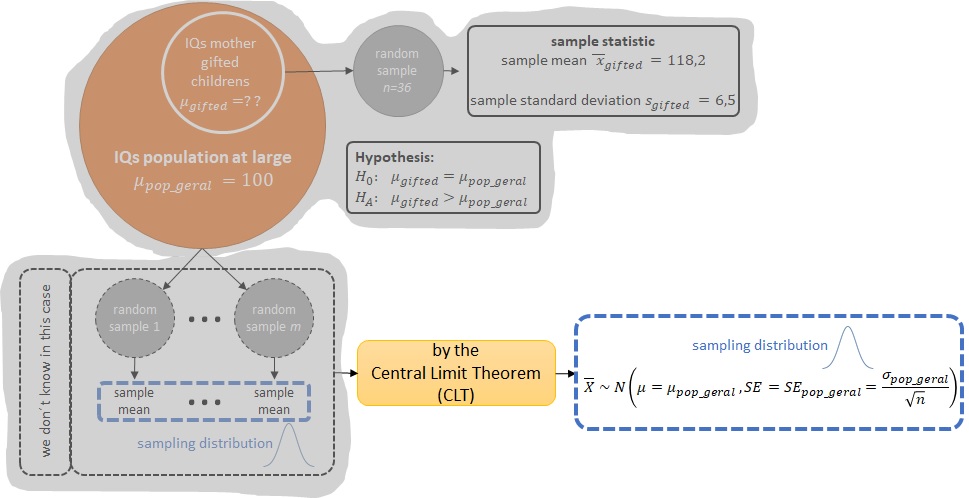
Bom, não temos a distribuição amostral (sampling distribution) das médias de QIs para a população geral, o que temos são:
- uma amostra aleatória (random sample) de $n = 36$ QIs de mães de crianças superdotadas;
- e o QI médio para a população geral $\mu_{pop\_geral}=100$.
Mas pelo Teorema Central do Limite (Central Limit Theorem - CLT), se as condições (1) e (2) forem verdadeiras para o nosso caso, então, podemos assumir que a distribuição amostral (sampling distribution) das médias de QIs para a população geral é da forma:
$$ \text{Médias QIs população geral} \sim N\left(mean=100, SE_{pop\_geral}=\frac{\sigma_{pop\_geral}}{\sqrt{n}}\right) $$Ainda precisamos calcular o valor do erro padrão (standard error) $SE_{pop\_geral}=\frac{\sigma_{pop\_geral}}{\sqrt{n}}$ para termos a forma completa da distribuição amostral (sampling distribution) das médias de QIs para a população geral. Ou seja, precisamos:
- do desvio padrão (standard deviation) $\sigma_{pop\_geral}$ da distribuição de QIs para a população geral;
- e do tamanho $n$ de alguma amostra aleatória (random sample) de QIs da população geral.
Bom, não temos acesso à distribuição de QIs para a população geral, logo, não temos o desvio padrão (standard deviation) $\sigma_{pop\_geral}$. Entretanto, podemos ter uma aproximação para $\sigma_{pop\_geral}$ através do desvio padrão (standard deviation) $s_{pop\_geral}$ de alguma amostra aleatória (random sample) de QIs da população geral.
Mas o que temos não é uma amostra aleatória (random sample) de QIs da população geral, mas sim uma amostra aleatória (random sample) de $n = 36$ QIs de mães de crianças superdotadas. Então, se, por um instante, assumirmos que a hipótese $H_0$ é verdadeira, estamos assumindo que o QI médio das mães de crianças superdotadas não é diferente do QI médio para a população geral, o que implica que podemos considerar a amostra aleatória (random sample) de $n = 36$ QIs de mães de crianças superdotadas como se fosse uma amostra aleatória (random sample) de QIs da população geral.
Então,
$$ \text{se } H_0 = True \enspace \Rightarrow \enspace \text{podemos assumir que } s_{pop\_geral} = s_{gifted} = 6,5 \enspace \Rightarrow \enspace SE_{pop\_geral} = \frac{\sigma_{pop\_geral}}{\sqrt{n}} \approx \frac{s_{pop\_geral}}{\sqrt{n}} = \frac{6,5}{\sqrt{36}} = 1,084 $$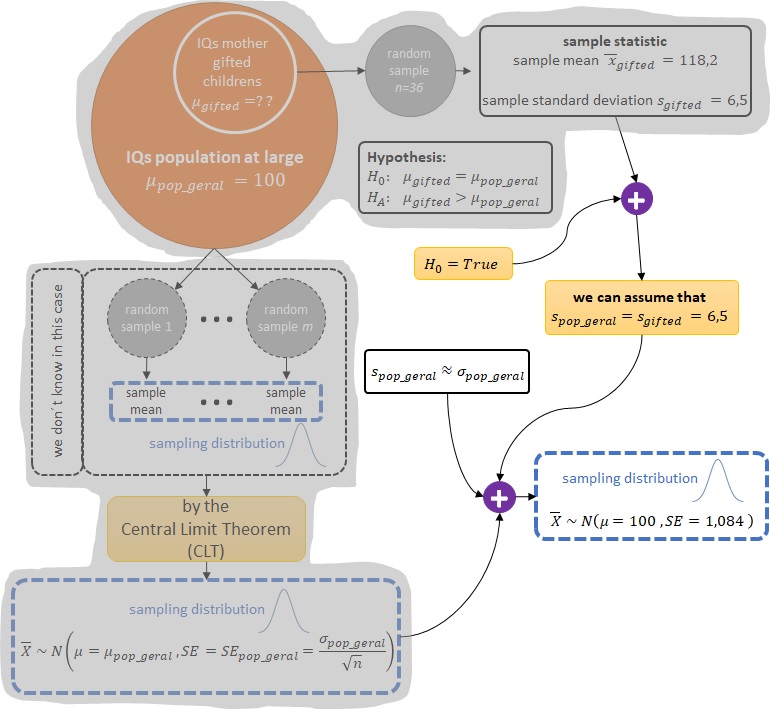
import numpy as np
std_observed_IQs_gifted = gifted_df.motheriq.std()
# estimated SE for IQs for population at large when H0 is true
estimated_SE = std_observed_IQs_gifted / np.sqrt(n)
print("Standard deviation of IQ of mothers of gifted children = {0:.1f}".format(std_observed_IQs_gifted))
print("Estimated standard error of IQs for the pop. at large when H0 is true = {0:.3f}".format(estimated_SE))
Logo, o nosso modelo que descreve as médias de QIs para a população geral quando assumimos que a hipótese $H_0$ é verdadeira é o:
$$ \text{se } H_0 = True \enspace \Rightarrow \enspace \text{Médias QIs população geral} \sim N\left(mean=100, SE_{pop\_geral}=1,084\right) $$from scipy import stats as st
mean_pop_IQ = 100
sampling_dist_mean_IQs_when_H0_is_true = st.norm(loc=mean_pop_IQ, scale=estimated_SE)
# import some dependencies to visualization with altair
import altair as alt
alt.renderers.enable('notebook') # for the notebook only (not for JupyterLab) run this command once per session
def draw_density_plot(distribution, distribution_name, x_axis_limits=None):
# Create the points to draw the probability density function
x_i = distribution.ppf(0.00000000000001)
x_f = distribution.ppf(0.99999999999999)
x = np.linspace(x_i, x_f, 100)
f_x = distribution.pdf(x)
# draw the density function f(x)
data = pd.DataFrame({'x': x, 'f(x)': f_x})
altX = 'x:Q'
if x_axis_limits is not None:
altX = alt.X('x:Q', scale=alt.Scale(domain=x_axis_limits))
density = alt.Chart(data).mark_line().encode(
x=altX,
y='f(x):Q'
).properties(title='{0}'.format(distribution_name))
return density
def draw_density_and_point_plot(distribution, distribution_name, obs_point, draw_area=False, type_area='left_area',
x_axis_limits=None):
density = draw_density_plot(distribution, distribution_name, x_axis_limits)
obs_value_mark_rule = density.mark_rule(color='red').encode(
x='obs_value:Q',
size=alt.value(1)
).transform_calculate(
obs_value=str(obs_point)
)
plot = density + obs_value_mark_rule
if draw_area:
if type_area == 'left_area':
predicate = alt.FieldLTEPredicate(field='x', lte=obs_point)
elif type_area == 'range_area':
obs_value_mark_rule2 = density.mark_rule(color='red').encode(
x='obs_value:Q',
size=alt.value(1)
).transform_calculate(
obs_value=str(-obs_point)
)
plot = density + obs_value_mark_rule + obs_value_mark_rule2
predicate = alt.FieldRangePredicate(
field='x',
range=[(obs_point if obs_point < 0 else -obs_point), (obs_point if obs_point > 0 else -obs_point)]
)
else:
predicate = alt.FieldGTEPredicate(field='x', gte=obs_point)
obs_value_mark_area = density.mark_area().encode(
x='x:Q',
y='f(x):Q'
).transform_filter(
predicate
)
plot = plot + obs_value_mark_area
return plot
distribution_name = "Sampling distribution when H0 is true ~ Normal(mean={0},sd={1:.3f})".format(mean_pop_IQ, estimated_SE)
diff = mean_observed_IQ_gifted - mean_pop_IQ
x_axis_limits = ((mean_pop_IQ-diff), (mean_pop_IQ+diff))
draw_density_plot(sampling_dist_mean_IQs_when_H0_is_true, distribution_name, x_axis_limits)
Logo, como já temos um modelo que representa a distribuição amostral (sampling distribution) das médias de QIs para a população geral quando assumimos que a hipótese $H_0$ é verdadeira, então, podemos calcular, utilizando este modelo (curva azul na figura abaixo), qual a probabilidade de observarmos uma média de QI igual ou mais extrema do que $118,2$ (marcação vermelha na figura abaixo).
draw_density_and_point_plot(
sampling_dist_mean_IQs_when_H0_is_true, distribution_name, mean_observed_IQ_gifted,
False, '', x_axis_limits
)
# use the CDF (cumulative distribution function) to calculate the probability
# that we will take a value grater than or equal to the observed mean
probability = 1.0 - sampling_dist_mean_IQs_when_H0_is_true.cdf(x=mean_observed_IQ_gifted)
print("Observed average IQ of mothers of gifted children = {0:.1f}".format(mean_observed_IQ_gifted))
print("Probability(IQ >= 118.2 | H0 is true) ~ {0} ({1}%)".format(probability, probability*100))
Então, se a hipótese $H_0$ for verdadeira e as condições (1) e (2) do Teorema Central do Limite (Central Limit Theorem - CLT) forem válidas para o nosso caso, a probabilidade de observarmos uma média de QI igual ou maior do que $118,2$ é de praticamente $0\%$. No entanto, os dados que temos mostram que observamos um QI médio $\bar{x}_{gifted}=118,2$. Logo:
- ou as condições (1) e (2) do Teorema Central do Limite (Central Limit Theorem - CLT) não são válidas para o nosso caso;
- ou temos uma evidência forte o suficiente para acreditar que a hipótese $H_0$ não seja verdadeira, mostrando que a hipótese válida é a $H_A$.
Vamos verificar se as condições (1) e (2) do Teorema Central do Limite (Central Limit Theorem - CLT) são válidas para o nosso caso.
A condição (1) exige que:
- (1a) o tamanho da amostra (sample size) seja suficientemente grande ($n > 30$ ou maior se os dados são consideravelmente enviesados), ou
- (1b) que a população (population) tenha uma distribuição normal.
Como temos uma amostra aleatória (random sample) de $n = 36$ QIs de mães de crianças superdotadas e o histograma desta amostra aleatória (random sample) não é consideravelmente enviesado, então, a condição (1a) está satisfeita, o que já satisfaz a condição (1).
# histogram of IQ of mothers of gifted children from this random sample
gifted_df.hist(column='motheriq', bins=(100,105,110,115,120,125,130,135))
A condição (2) exige que:
- (2) as observações da amostra (sample) sejam independentes.
A independência de observações em uma amostra é viabilizada pelo uso de amostragem aleatória (no caso de estudos observacionais) ou atribuição aleatória (no caso de experimentos). O nosso caso trata de um estudo observacional e, conforme informado no enunciado, os pesquisadores obtiveram uma amostra aleatória (random sample) de $n = 36$ QIs de mães de crianças superdotadas. Logo, a condição (2) também está safisfeita.
Portanto, concluímos que temos uma evidência forte o suficiente para acreditar que a hipótese $H_0$ não é verdadeira, mostrando que a hipótese válida é a $H_A$, ou seja, a de que o QI médio das mães de crianças superdotadas é maior do que o QI médio para a população geral.
Hipóteses Nula e Alternativa¶
No exemplo anterior, as notações $H_0$ e $H_A$ para as hipóteses não foram utilizadas à toa. Denota-se por $H_0$ a hipótese nula (null hypothesis) e por $H_A$ a hipótese alternativa (alternative hypothesis).
A hipótese nula (null hypothesis) $H_0$ geralmente representa uma posição cética ou uma perspectiva de nenhuma diferença, por exemplo, o QI médio das mães de crianças superdotadas não é diferente do QI médio para a população geral.
A hipótese alternativa (alternative hypothesis) $H_A$ geralmente representa uma nova perspectiva, como a possibilidade de que houve uma mudança, por exemplo, o QI médio das mães de crianças superdotadas é maior do que o QI médio para a população geral.
Além disto, as hipóteses sempre devem ser construídas em relação aos parâmetros da população (population) -- por exemplo, a média da população (population mean) $\mu$ -- e não em relação às estatísticas das amostras (sample statistics) -- por exemplo, a média da amostra (sample mean) $\bar{x}$.
Observe que o parâmetro da população (population) é desconhecido, enquanto que a estatística da amostra (sample statistic) é medida utilizando os dados observados e, portanto, não há razão para criar hipóteses sobre isso.
Utilizando o escore-z (z-score)¶
No exemplo anterior, a partir do momento em que assumimos que a distribuição amostral (sampling distribution) das médias de QIs para a população geral é uma normal:
$$ \text{se } H_0 = True \enspace \Rightarrow \enspace \text{Médias QIs população geral} \sim N\left(mean=100, SE_{pop\_geral}=1,084\right) $$então, ao invés de verificar:
- (a) Qual a probabilidade de observarmos uma média de QI igual ou mais extrema do que $118,2$ dentro do modelo $N\left(mean=100, SE_{pop\_geral}=1,084\right)$?
podemos transformar esta pergunta em:
- (b) Qual a probabilidade de observarmos uma distância em unidades de QI igual ou mais extrema do que $118,2 - 100 = 18,2$ dentro do modelo $N\left(mean=100, SE_{pop\_geral}=1,084\right)$?
Como a distribuição é uma normal e estamos medindo a distância de um valor ($118,2$) para a média de uma normal ($\mu=100$), então, é possível generalizar este conceito para trabalharmos com o escore-z (z-score), que como já vimos aqui, é também uma medida de distância, no caso, o número de desvios padrão (standard deviations) acima (positivo) ou abaixo (negativo) de uma média de uma distribuição normal.
A generalização aqui ocorre a partir do momento em que substituímos uma distância ($18,2$) dada em unidades de QI por uma distância dada em desvios padrão (standard deviations), em outras palavras, uma distância dada em escores-z (z-scores).
distance_in_IQ_units = mean_observed_IQ_gifted - mean_pop_IQ
std_of_our_model_when_H0_is_true = estimated_SE
distance_in_standard_deviations = distance_in_IQ_units / std_of_our_model_when_H0_is_true
observed_z_score = distance_in_standard_deviations
print("Distance from the mean in IQ units = {0:.1f}".format(distance_in_IQ_units))
print("Standard deviation of our model when H0 is true (i.e. the estimated SE) = {0:.3f}".format(
std_of_our_model_when_H0_is_true))
print("Observed z-score (i.e. distance in standard deviations) = {0:.2f}".format(observed_z_score))
Assim, a pergunta passa a ser: Qual a probabilidade de observarmos um escore-z (z-score) igual ou mais extremo do que $16,76$?
Uma vez que já sabemos que os valores de escore-z (z-score) são distribuídos de acordo com a distribuição normal padrão (standard normal distribution) que também é conhecida como distribuição z (z distribution), então:
z_distribution = st.norm(loc=0, scale=1)
distribution_name = "z distribution ~ Normal(mean=1,sd=0)"
x_axis_limits = (-observed_z_score, +observed_z_score)
draw_density_and_point_plot(z_distribution, distribution_name, observed_z_score, False, '', x_axis_limits)
# use the CDF (cumulative distribution function) to calculate the probability
# that we will take a value grater than or equal to the observed z-score
probability = 1.0 - z_distribution.cdf(x=observed_z_score)
print("Observed z-score = {0:.2f}".format(observed_z_score))
print("Probability(z-score >= 16.76 | H0 is true) ~ {0} ({1}%)".format(probability, probability*100))
Logo, utilizando o escore-z (z-score), chegaríamos na mesma conclusão de antes, ou seja:
Se a hipótese nula (null hypothesis) $H_0$ for verdadeira e as condições (1) e (2) do Teorema Central do Limite (Central Limit Theorem - CLT) forem válidas para o nosso caso, a probabilidade de observarmos um escore-z (z-score) igual ou maior do que $16,76$ é de praticamente $0\%$. No entanto, os dados que temos mostram que observamos um escore-z (z-score) de $16,76 = \frac{\bar{x}_{gifted}-\mu_{pop\_geral}}{\hat{se}_{pop\_geral}}$.
E como já sabemos que as condições (1) e (2) do Teorema Central do Limite (Central Limit Theorem - CLT) são válidas para o nosso caso, então:
Concluímos que temos uma evidência forte o suficiente para acreditar que a hipótese nula (null hypothesis) $H_0$ não é verdadeira, mostrando que a hipótese alternativa (alternative hypothesis) $H_A$ é válida, ou seja, a de que o QI médio das mães de crianças superdotadas é maior do que o QI médio para a população geral.
O p-valor (p-value)¶
Nas duas abordagens anteriores (sem o uso e com o uso do z-score) tivemos que calcular uma probabilidade que, no caso deste exemplo das mães de crianças superdotadas, nos ajudou a rejeitar a hipótese nula (null hypothesis) $H_0$ em detrimento da hipótese alternativa (alternative hypothesis) $H_A$, ou seja, vimos que:
- (sem o uso do z-score): se a hipótese nula (null hypothesis) $H_0$ for verdadeira e as condições (1) e (2) do Teorema Central do Limite (Central Limit Theorem - CLT) forem válidas para o nosso caso, a probabilidade de observarmos uma média de QI igual ou maior do que $118,2$ é de praticamente $0\%$.
- (com o uso do z-score): se a hipótese nula (null hypothesis) $H_0$ for verdadeira e as condições (1) e (2) do Teorema Central do Limite (Central Limit Theorem - CLT) forem válidas para o nosso caso, a probabilidade de observarmos um escore-z (z-score) igual ou maior do que $16,76$ é de praticamente $0\%$.
Em outras palavras, trata-se de uma probabilidade condicional (conditional probability) denominada de p-valor (p-value) onde assumimos que a hipótese nula (null hypothesis) $H_0$ é verdadeira, ou seja:
- (sem o uso do z-score): $\text{p-value} = \Pr\left( \bar{x} \geq 118,2 \;\middle\vert\; H_0 = True \right) \approx 0$.
- (com o uso do z-score): $\text{p-value} = \Pr\left( \text{z-score} \geq 16,76 \;\middle\vert\; H_0 = True \right) \approx 0$.
# use the CDF (cumulative distribution function) to calculate the probability
# that we will take a value grater than or equal to the observed mean
p_value = 1.0 - sampling_dist_mean_IQs_when_H0_is_true.cdf(x=mean_observed_IQ_gifted)
print("Observerd average IQ of mothers of gifted children = {0:.1f}".format(mean_observed_IQ_gifted))
print("p-value = Probability(IQ >= 118.2 | H0 is true) ~ {0} ({1}%)".format(p_value, p_value*100))
print("-------------------------")
# use the CDF (cumulative distribution function) to calculate the probability
# that we will take a value grater than or equal to the observed z-score
p_value = 1.0 - z_distribution.cdf(x=observed_z_score)
print("Observed z-score = {0:.2f}".format(observed_z_score))
print("p-value = Probability(z-score >= 16.76 | H0 is true) ~ {0} ({1}%)".format(p_value, p_value*100))
Esta probabilidade condicional (conditional probability) quantifica a força da evidência contra a hipótese nula (null hypothesis) $H_0$ e a favor da hipótese alternativa (alternative hypothesis) $H_A$. Quanto menor o valor do p-valor (p-value) mais forte é a evidência contra a hipótese nula (null hypothesis) $H_0$, uma vez que o p-valor (p-value) é uma probabilidade condicionada à validade da hipótese nula (null hypothesis) $H_0$.
Mas o quão pequeno deve ser o valor do p-valor (p-value) para que possamos rejeitar a hipótese nula (null hypothesis) $H_0$ e ficar com a hipótese alternativa (alternative hypothesis) $H_A$? Este é um assunto para um outro tópico :).
Pela definição da wikipedia:
In statistical hypothesis testing, the p-value or probability value or asymptotic significance is the probability for a given statistical model that, when the null hypothesis is true, the statistical summary (such as the sample mean difference between two compared groups) would be greater than or equal to the actual observed results. (Fonte: https://en.wikipedia.org/wiki/P-value)
ou seja, para o nosso exemplo:
- (sem o uso do z-score):
- o modelo estatístico (statistical model): $\bar{X} \sim N\left(mean=100, std=1,084\right)$
- a estatística utilizada (statistical summary): $\bar{x}_{observed} = 118,2$
- o p-valor (p-value): $\Pr\left( \bar{x} \geq 118,2 \;\middle\vert\; H_0 = True \right) \approx 0$
- (com o uso do z-score):
- o modelo estatístico (statistical model): $\text{z-score} \sim N\left(mean=0, std=1\right)$
- a estatística utilizada (statistical summary): $\text{z-score}_{observed} = 16,76$
- o p-valor (p-value): $\Pr\left( \text{z-score} \geq 16,76 \;\middle\vert\; H_0 = True \right) \approx 0$
Então, de maneira mais genérica, podemos definir o p-valor (p-value) como:
$$ \text{p-value} = \Pr\left( \text{observed or more extreme sample statistic} \;\middle\vert\; H_0 = True \right). $$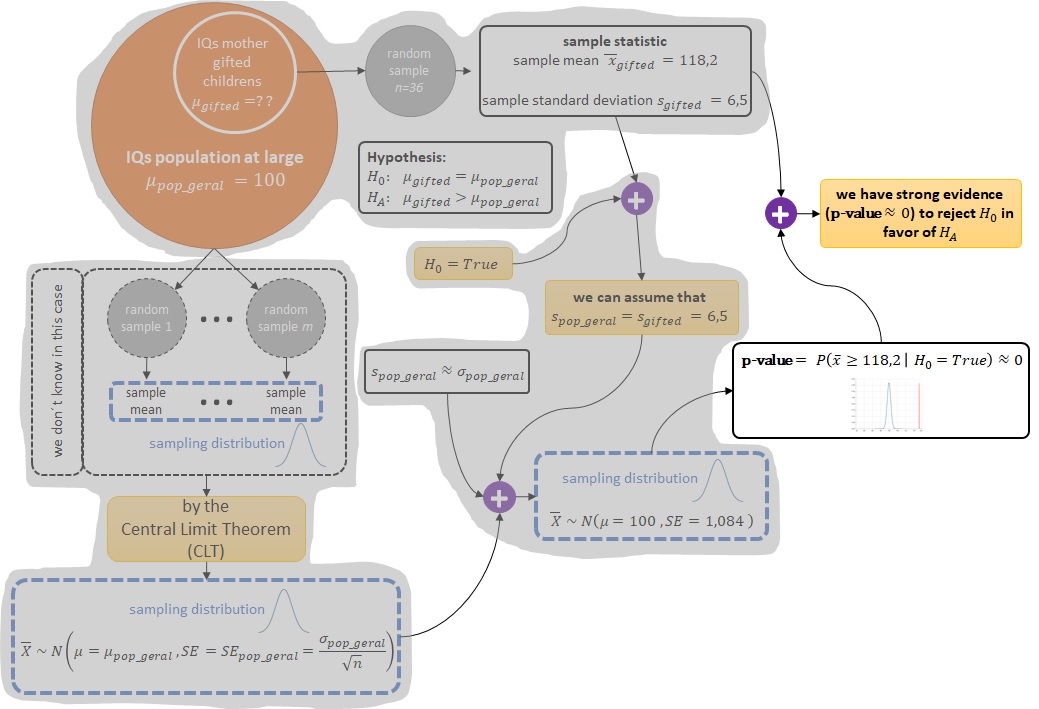
O teste Z (Z test)¶
Todo o procedimento que fizemos anteriormente e tudo o que assumimos ao longo do procedimento para chegar à conclusão de que o QI médio das mães de crianças superdotadas é maior do que o QI médio para a população geral, na prática, foi um teste Z (Z test).
Pela wikipedia:
A Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. (Fonte: https://en.wikipedia.org/wiki/Z-test)
Utilizando Python (e talvez qualquer outra linguagem de programação com bibliotecas/pacotes estatísticos), com apenas uma linha de código (como a abaixo ztest(.)) podemos executar um teste Z (Z test) e chegar na mesma conclusão de antes:
from statsmodels.stats.weightstats import ztest
# run a one-sided Z test
test_statistic, p_value = ztest(x1=np.array(gifted_df.motheriq), x2=None, value=mean_pop_IQ, alternative='larger')
print("test statistic (in this case, the z-score) = {:.2f}".format(test_statistic))
print("p-value = {:.3f}".format(p_value))
Ao executar o teste Z (Z test) obtivemos como resultado:
- uma estatística de teste (test statistic) -- que no caso é o escore-z (z-score) -- de $16,76$, ou seja, idêntico ao escore-z (z-score) que calculamos anteriormente;
- um p-valor (p-value) praticamente igual a $0$, ou seja, idêntico ao p-valor (p-value) que calculamos anteriormente.
e tudo isto com apenas uma linha de código ... e é "aqui que mora o perigo", ou seja, é tão fácil e rápido utilizar esta "apenas uma linha de código" que muitas pessoas esquecem (ou não sabem) as premissas por trás do uso desta "apenas uma linha de código" e, como consequência, podem acabar tirando conclusões equivocadas. Talvez este seja o motivo do nome Danger Zone! no famoso diagrama de Venn abaixo.
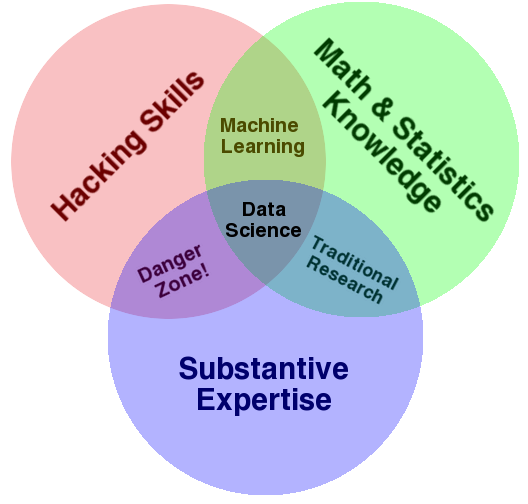(Fonte: Image of Data Science Venn Diagram, by Drew Conway, licensed under a Creative Commons Attribution-Attribution-NonCommercial.)
Então, vamos listar aqui tudo o que tivemos que assumir para executar o teste de hipótese (hypothesis testing) -- na prática o teste Z (Z test) -- do exemplo do QI médio das mães de crianças superdotadas:
- Que as condições (1) e (2) impostas pelo Teorema Central do Limite (Central Limit Theorem - CLT) são válidas para o nosso caso, ou seja:
- (1a) o tamanho da amostra (sample size) é suficientemente grande ($n > 30$ ou maior se os dados são consideravelmente enviesados), ou
- (1b) sabe-se de antemão que a população (population) tem uma distribuição normal, e
- (2) as observações da amostra (sample) são independentes.
- Que a distribuição amostral (sampling distribution) das médias de QIs é aproximadamente normal (nearly normal).
- Que o desvio padrão (standard deviation) $s$ da amostra aleatória (random sample) -- que utilizamos para calcular a estimativa $\hat{se}$ para o erro padrão (standard error) $SE=\frac{\sigma}{\sqrt{n}}$ da distribuição amostral (sampling distribution) das médias de QIs -- é uma boa aproximação para o desvio padrão (standard deviation) $\sigma$ da população (population);
- Que a estimativa $\hat{se}$ também é uma boa aproximação para o erro padrão (standard error) $SE=\frac{\sigma}{\sqrt{n}}$ da distribuição amostral (sampling distribution) das médias de QIs.
Ou seja, por trás do uso desta "apenas uma linha de código" temos todas as premissas anteriores que tivemos que assumir para poder utilizar o teste Z (Z test).
Resumo¶
R1. Em teste de hipótese (hypothesis testing) avaliamos duas afirmações concorrentes:
- A hipótese nula (null hypothesis) $H_0$ que geralmente representa uma posição cética ou uma perspectiva de nenhuma diferença;
- A hipótese alternativa (alternative hypothesis) $H_A$ que geralmente representa uma nova perspectiva, como a possibilidade de que houve uma mudança.
R2. As hipóteses sempre devem ser construídas em relação aos parâmetros da população (population) -- por exemplo, a média da população (population mean) $\mu$ -- e não em relação às estatísticas das amostras (sample statistics) -- por exemplo, a média da amostra (sample mean) $\bar{x}$.
R3. A independência de observações em uma amostra é viabilizada pelo uso de amostragem aleatória (no caso de estudos observacionais) ou atribuição aleatória (no caso de experimentos).
R4. O p-valor (p-value) é uma probabilidade condicional (conditional probability) que quantifica a força da evidência contra a hipótese nula (null hypothesis) $H_0$. Quanto menor o valor do p-valor (p-value) mais forte é a evidência contra a hipótese nula (null hypothesis) $H_0$, uma vez que o p-valor (p-value) é uma probabilidade condicionada à validade da hipótese nula (null hypothesis) $H_0$.
- $\text{p-value} = \Pr\left( \text{observed or more extreme sample statistic} \;\middle\vert\; H_0 = True \right).$
R5. Teste de hipótese (hypothesis testing) para uma única média via o teste Z (Z test):
- Estabeleça as hipóteses:
- $H_0: \mu = \text{null value}$
- $H_A: \mu < \text{ou} > \text{ou} \neq \text{null value}$
- Calcule a estimativa pontual (point estimate): $\bar{x}$
- Verifique se as condições do Teorema Central do Limite (Central Limit Theorem - CLT) são válidas:
- (1a) o tamanho da amostra (sample size) é suficientemente grande ($n > 30$ ou maior se os dados são consideravelmente enviesados), ou
- (1b) sabe-se de antemão que a população (population) tem uma distribuição normal, e
- (2) as observações da amostra (sample) são independentes.
- Calcule o erro padrão (standard error):
- $SE = \frac{\sigma}{\sqrt{n}}$, se tiver acesso ao desvio padrão (standard deviation) $\sigma$ da população (population);
- $\hat{se} = \frac{s}{\sqrt{n}}$, caso contrário.
- Calcule a estatística de teste (test statistic):
- $\text{z-score}_{observed} = \frac{\bar{x} - \mu}{SE}$, ou
- $\text{z-score}_{observed} = \frac{\bar{x} - \mu}{\bar{se}}$.
- Calcule o p-valor (p-value):
- $\text{p-value} = \Pr\left( \text{z-score} \geq \text{z-score}_{observed} \;\middle\vert\; H_0 = True \right)$
- onde $\text{z-score} \sim N\left(mean=0, std=1\right)$
- Com base no valor calculado para o p-valor (p-value), determine se a hipótese $H_0$ deve ou não ser rejeitada:
- Lembre-se, quanto menor o valor do p-valor (p-value) mais forte é a evidência contra a hipótese nula (null hypothesis) $H_0$.
< Tamanho da Amostra, Variância e Viés | Conteúdo | [A ser definido] >